GNN论文精选-第二组
DropEdge Towards Deep Graph Convolutional Networks On Node Classification
Drop Edge
Drop Edge[1],其方法顾名思义,就是丢弃图中的边。
具体来说,对于一个邻接矩阵 $A$ ,对于其中的每一个元素以 $p$ 的概率置0。 这看起来和 dropout 如出一辙,事实上在实现的时候,也是采用 dropout 算子来对邻接矩阵进行处理的(dropout 算子在每一轮梯度下降时,使每一个神经元以 $p$ 的概率随机置0,使得被置0的神经元无法进行梯度更新)。
这可以说就是该方法的全部了。没错,就是这么简单。那么作者又是怎么把这么一个两句话就能讲完的方法写成一篇论文的呢?故事由此开始。
Overfitting and Oversmoothing
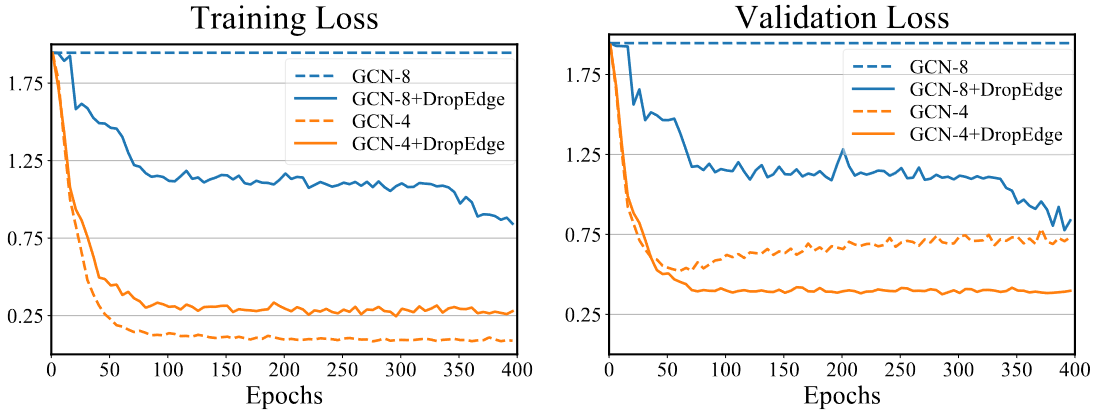
Overfitting 是机器学习的常用概念了,具体来说就是训练集上的效果不错,但在测试集上的效果却很差。Oversmoothing 则是由Li等人[2]提出来的概念,而后被[[Notes for Collection 1#JKN Representation Learning on Graphs with Jumping Knowledge Networks|JKN]]、[[Notes for Collection 1#PPNP Predict then Propagate Graph Neural Networks meet Personalized PageRank|PPNP]]等模型的论文里具体说明并尝试解决的问题。具体来说,它是指GNN在层数增多后,由于特征传播与聚合的操作,所有特征表示都趋向一个稳定值,其原理类似于随机游走。这使得后期的训练变得困难,具体表现为梯度下降优化时发生梯度消失,从而使得训练损失难以下降。
而 Drop Edge 的引入可以改善这2个问题。
Overfitting
关于过拟合,作者定性地说明了该方法是通过对数据的随机扰动而对数据进行增强改善,其类似于图像分类中对图像进行拉伸、旋转等变换。另外,这种数据扰动从期望上看与原数据相比是无偏的。如果我们以概率 $p$ 删除边,则 DropEdge 只会将邻居聚合的期望上乘上 $(1-p)$(因为采样符合伯努利分布),而这个乘数将在对其归一化后实际上消失了,因此,DropEdge不会改变邻居聚合的期望。综上,DropEdge可以看作是一个无偏数据增强技术。
Oversmoothing
对于过度平滑,作者花了较大笔墨去证明。其过程有些复杂,暂时看不太懂[[[WHY]]]。
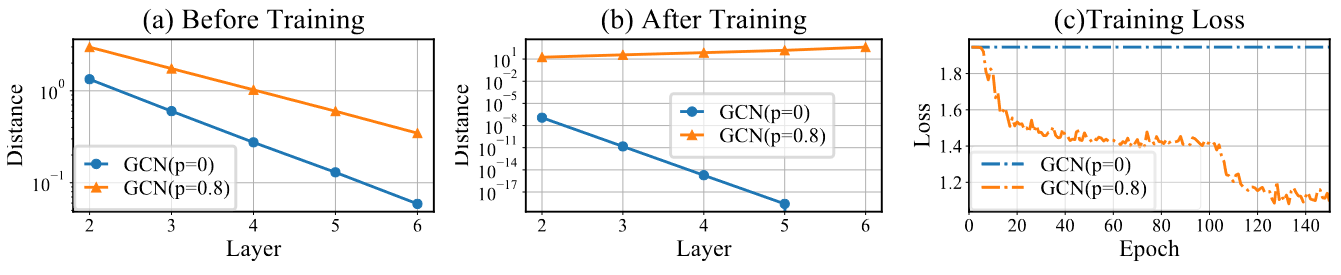
但仍然可以从实验的角度来验证这一点。实验中,作者使用该层结点表示与上一层结点表示的欧几里得距离来衡量。由下图可以知道,在训练之前(模型采用初始化权重),可以发现经过DropEdge后,相邻两层结点表示的差距始终大于未使用DropEdge的模型。图b为经过150个epoch训练后的结果,发现在5和6层,其差异为0。从训练损失来看,没有通过DropEdge根本训练不动,原因很简单,第5和第6层差异为0,从而发生了严重的梯度消失现象,无法使用梯度下降优化。
Hyperparameter
该论文的超参数也是值得一提的。作者使用的超参数由下表列出。

其中withloop为方法self feature modeling,来源于Fout等人的工作[3],其公式如下。
$$ H^{(l+1)} = \sigma (\tilde AH^{(l)}W^{(l)} + H^{(l)}W^{(l)}_{self})$$
表中的normalization为传播模型,它使用了如下4种模式,都是比较流行的传播模式。

Dropout and Layer-wise DropEdge
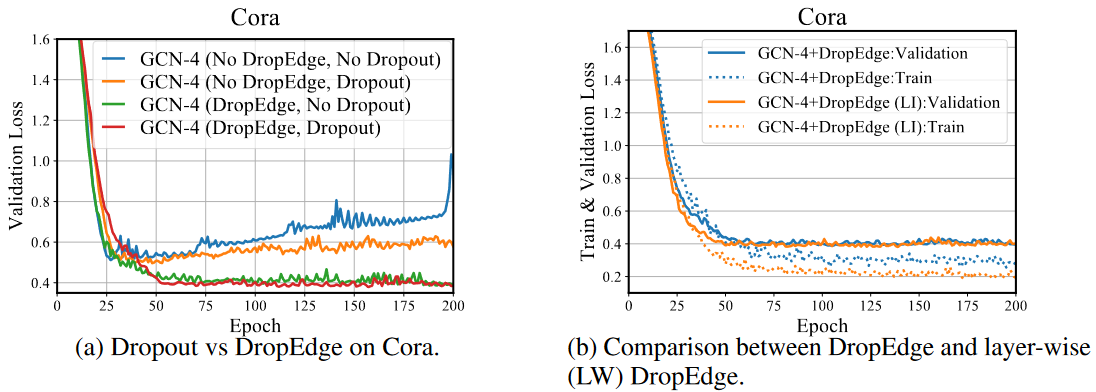
Dropout 可以看作是 DropEdge 的一种特殊情形,因为当结点特征被丢弃,那么所连接的边也就没了。作者通过实验说明了 Dropout 和 DropEdge 有互补的作用,联合使用可以使得效果更好。
此外,作者还提出了 Layer-wise DropEdge。上述所使用的 DropEdge 都是针对一整个模型的,也就是说,每一次梯度下降使用一次 DropEdge 得到的 $A_{drop}$ 是针对模型的所有层。而Layer-wise 指的是每一层都独立使用一次 DropEdge,也就是说每一层的 $A_{drop}$ 是不一样的。作者通过实验说明,Layer-wise DropEdge缺失可以降低训练损失,但在验证集上的损失并没有下降。因此,作者更建议使用对面向模型的 DropEdge,而非 Layer-wise,这样可以防止过拟合,并减少不必要的计算。
Conclusion
该论文借鉴了 dropout,仅仅对模型进行了一个很简单的改动,却在各个数据集上取得了非常不错的效果。也从理论上证明作者的方法可以一定程度上缓解Over Smoothing的问题。文章也教会我们如何将一个简短的方法写长,即使用大量的分析、比较,再辅之以理论证明,就可以讲好一个简单又精彩的故事。
AdaGCN Adaboosting Graph Convolutional Networks into Deep Models
Adaboost
论文首先是借鉴了 Adaboost 方法。
[[Ensemble Learning#Random Forest|Adaboost]] 是一种集成学习的方法。该方法可以使一组弱分类器组成一个强的集成分类。但由于其用于二分类,作者使用它的多分类形式,SAMME[4]。

其区别就在于 $\alpha$ 的式子增加了 $log(K-1)$ 这一项。直观地去理解,会发现,当每一个类别的误差率大于 $\frac{1}{K}$ 时,$\alpha$ 就会大于0,这符合原来二分类的性质。
为了方便计算以及增强模型的收敛性质,作者使用它的一个改良版本 SAMME.R (R for real)。以下为它的算法描述。

它的主要区别在于将误差率的公式,由原来的指示函数,更改为一个加权概率函数。随后的权重计算公式以及加权分类结果是通过解决以下优化方程得到的。
$$
\begin{align}
&\min _{h(x)} \operatorname{E} \bigg( \exp \bigg( -\frac{1}{K} Y^T\big(f^{(m−1)}(x)+h(x)) \bigg) |x \bigg) \
&subjecttoh_1(x)+···+ h_K(x)=0
\end{align}
$$
该方程旨在最小化集成分类器的指数损失。其中还需注意的一个是,其中的数据标签的向量$y =(y_1,…,y_K )^T$,它并不是一个 0/1 向量,它的定义为
$$
yk =
\left{
\begin{align}
&1, &&ifc = k, \c \ne k.\
&−\frac{1}{K−1} , &&if
\end{align}
\right.
$$
RNN-like
该论文提出的模型架构可以概括为:
$$
\begin{align}
&\hat{A}^lX = \hat A·(\hat A^{l−1} X ) \
&Z^{(l)} = f {\theta}^{(l)} (\hat A^l X ) \
&Z = \operatorname{AdaBoost}(Z^{(l)}) %不能有多余的空行,不然在网页中也可能除左
\end{align}
$$
其中 $f{\theta}^{(l)}$ 为非线性函数,比如说2层的神经网络$f^{(l)}{\theta}(\hat A^l X) = \operatorname{ReLU}(\hat A^l XW ^{(0)})W^{(1)}$。但是,这里需要注意的是,该模型和Adaboost有一个重要区别,那就是对于所有的 $l$ 来说,$f{\theta}^{(l)}$ 使用 $\theta$ 参数是基于上一层分类器 $f_{\theta}^{(l-1)}$。而一般的Adaboost各个基分类器的参数都是独立的。
模型架构可以由如下图表示。
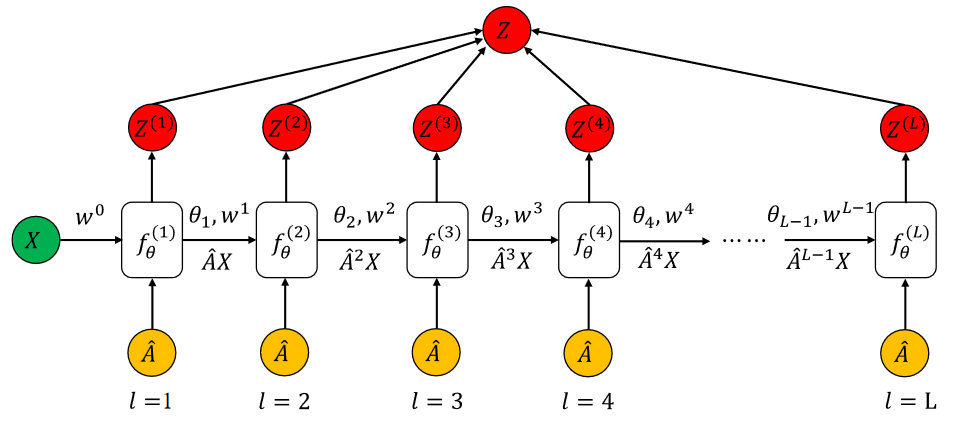
可以看到,这样的结构和RNN非常相像,每一层都由来自于上一层的输入,使用的 $\theta$ 参数是共用的。也就是说,AdaGCN中每一层基分类器 $f_{\theta}^{(l)}$ 都是在上一层分类器 $f_{\theta}^{(l-1)}$ 的参数上进行更行的,这一点是和Adaboost的一个重要区别。
Algorithm
以下为算法的伪代码。

该流程基本在参数更新中,基本仿照了SAMME.R的算法流程。值得注意的是,该算法和我们之前所看到的那些模型有个重要的不同,那就是最后的输出不是一个模型,而是一个最终的预测结果,这一点是有些奇怪的。
因为常理来说,在训练过程之后,我们将得到一个模型,最终再使用这个模型运用到验证集、测试集上。也就是说训练和预测应当是分开的,但这个算法流程貌似是合起来的。但如果我们回想一下GCN的训练过程也许就能明白,GCN的训练是一种transductive learning,也就是说其预测的东西都是模型所见过的。所以GCN训练时,将整个数据集都输入了进去,但只使用少量标签进行训练。事实上,每次训练都可以得到整个数据集的标签,但计算损失时仅使用训练数据的标签。
那么算法也同理,训练时输入整个数据集(包括训练集、验证集、测试集),但计算损失、拟合参数时只是用训练集部分的标签。因此它的输出也自然可以是整个数据集的标签。但如果偏要将训练和预测完分离开来,则需要记录训练时每一层分类器的参数$\theta$,还要在预测时将第3、6、7步去掉。
Computational Comlexity and Netowrk Depth
AdaGCN的计算复杂度,主要的有点就是可以提前计算传播矩阵,也就是对于第 $l$ 层来说,$B^{l}=\hat A^{l}X$ 可以被提前计算,这使得不需要在训练的每个epoch都再算一遍,这和SGC类似。
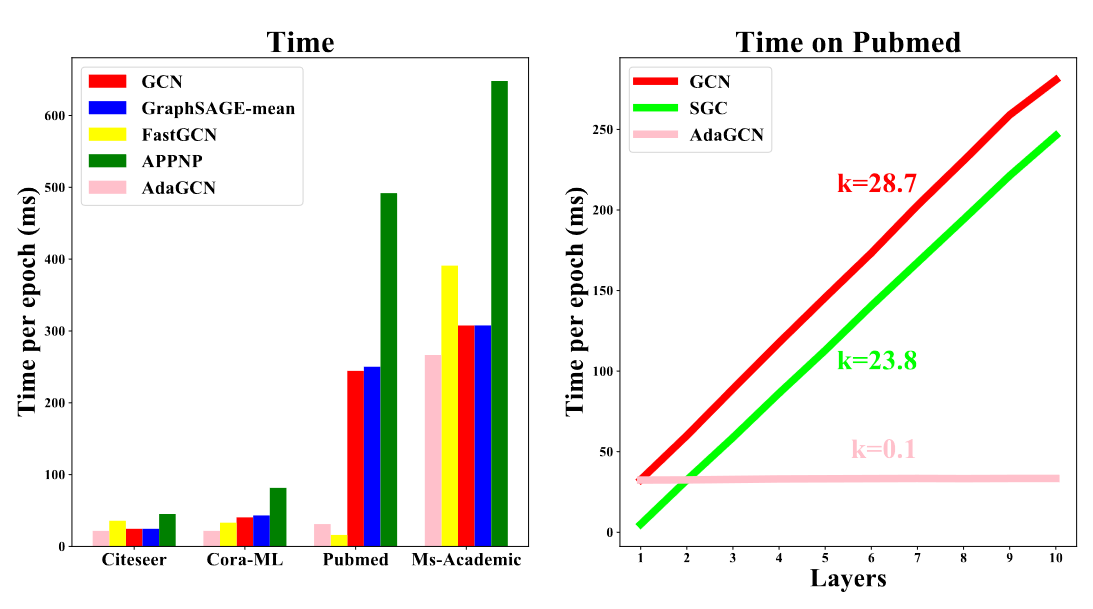
经过作者的实验,也确实展现出它的高效。但是上面右边这张图就有些奇怪了,随着网络层次的加深,SGC每个epoch训练时间的增长远超AdaGCN,这不禁令人怀疑。因为对于SGC来说,同样是提前计算了传播矩阵和特征矩阵的乘积,并且其算法要比AdaGCN简单得多,怎么可能会比它慢呢?个人感觉,作者对SGC并没有采取提前计算的方法。
此外作者同样指出,AdaGCN虽然每个epoch训练时间比较短,但它所需要的epoch却更多一些。
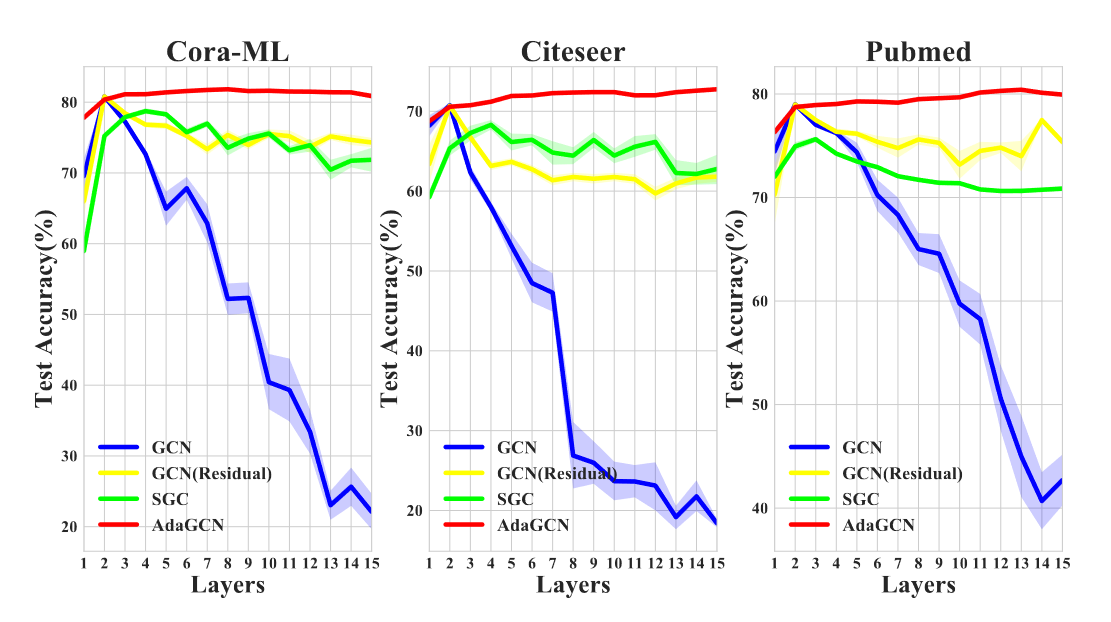
此外,作者还比较了各个模型加大深度后性能的变化。这里需要注意的是,模型的深度指的是特征传播的深度。事实上,AdaGCN有2个深度,一个是基分类器的数量,也就是作者所谓的深度,还有一个是 $f_{\theta}$ 这一非线性函数,事实上它可以是个深度神经网络,同样也可以有深度。作者的模型,也确实将网络深度与传播深度分离开来了,这一点和[[Notes for Collection 1#PPNP Predict then Propagate Graph Neural Networks meet Personalized PageRank|PPNP]]比较类似。
在结果上,随着深度加深,其性能确实不会有什么衰减,一定程度上减轻了Oversmoothing的问题,甚至可能略有提升。
不同于其他论文,改论文还讨论了模型的深度该如何确定,也就是基分类器的个数如何选择。其引用了[[#附录#Vapnik–Chervonenkis dimension|VC-dimesion]]的理论,大该是想说明,随着基分类器个数的增加,模型的VC维上界也会增大,从而提高模型过拟合的风险。但是总之,作者也就是说在实践中用交叉验证的方法来确定模型深度(讲了和没讲一样)。
Connection with PPNP and APPNP.
作者认为,AdaGCN是自适应版本的APPNP。这里我没怎么看懂。我的理解时在传播过程中,APPNP里MLP参数是固定的,而AdaGCN则不是,每一层传播的参数不一样,即基分类器参数不同。因此他更具备适应性。另外有一点和APPNP是一样的,就是MLP的深度和传播深度是独立的。
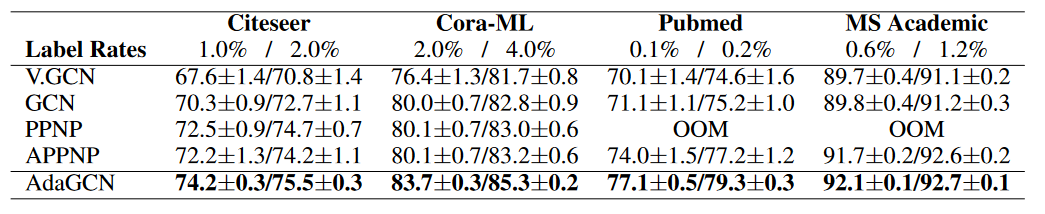
作者通过实验比较,发现在低标签率的情况下,其效果也超过APPNP(这曾是APPNP的优点之一)。
Conclusion
AdaGCN借鉴集成学习中Adaboost的方法,设计了一个RNN-like的算法。其效率和性能都比较强。
GCNII Simple and Deep Graph Convolutional Networks
Residual Connection and Identity Map
GCNII 的模型可以由如下公式表示:
$$
H^{(l+1)} =\sigma\bigg(\bigg( (1−\alpha_l) \tilde PH^{(l)} +\alpha_l H^{(0)}\bigg)\bigg( (1−\beta_l)I_n +\beta_l W^{(l)}\bigg)\bigg)
$$
它由2部分组成:
- 初始层残差连接:$(1−\alpha_l) \tilde PH^{(l)} +\alpha_l H^{(0)}$,注意这里的 $H^{(0)}$ 不必是 $X$,它可以是 $X$ 经过线性变换的结果,如 $XW$。
- 自身映射:$(1−\beta_l)I_n +\beta_l W^{(l)}$
著名的 ResNet 就是利用残差连接来避免梯度消失问题,从而使得神经网络可以做得很深。但 ResNet 的残差连接,是和前几层做加法运算,这事实上在 GCN 中就已经尝试过使用这种方法了,确实在一定程度上可以缓解 Oversmoothing 的问题,但效果随着深度地加深,并没有变好。
于是在本文使用的残差是与初始层做的残差。事实上这一迭代形式和 [[Notes for Collection 1#PPNP and APPNP|APPNP]] 非常相似。这里提供了一个新的视角来理解APPNP,即和初始层做残差连接的神经网络。但和 APPNP 的区别也十分明显,APPNP 在传播过程并没有参数学习的过程,但 GCNII 每一次传播乘上参数矩阵,并使用非线性函数压缩。也就是说,在 GCNII 中,它并没有讲特征传播的深度和神经网络的深度独立开来,二者是统一的。
这里 GCNII 每一层使用的参数矩阵包含了一个自身的映射。从优化的角度来看,它有2个作用[5]:1. 使得参数矩阵 $W$ 的范数很小,这样可以使用较大的正则化系数防止过拟合;2. 优化方程的驻点就是全局最小值。
另外作者还给出了 $\beta_l$ 的选取,它的选择对于不同深度来说应当使不以言的,随着深度的加深,为了防止过拟合以及梯度消失,$\beta_l$ 应当变小,让单位矩阵占据更大比重。作者给出了调整公式:
$$
\beta_l=log(\frac{\lambda}{l}+1)\approx\frac{\lambda}{l}
$$
其中 $\lambda$ 时超参数。但他貌似没有说原因,我也不知道这公式是哪来的[[[WHY]]]。
另外作者还介绍了自身映射和压缩感知(Compressive Sensing)领域中的算法 ISTA (或者iSTA)进行了比较。ISTA 是线性问题的逆问题,通过求解以下 Lasso 正则化形式的优化方程
$$
\min_{x\in \mathcal{R}^n} \frac{1} {2} ‖Bx − y‖2^2 + \lambda‖x‖_1.
$$
与我们常见的线性回归问题不同,这里 $B,y$ 是已知量,而 $x$ 则是待求量。它可以看作是一个信号重建的问题,经过亚采样的信号进行重建。和梯度下降类似,最终可以通过如下的迭代求解 $x$。
$$
x{t+1} = P_{\mu_tλ} (x_t − \mu_tB^T Bx_t + \mu_tB^T y) ,
$$
$P_β(·)$ 是一个带阈值的线性函数,他的曲线如下图所示。
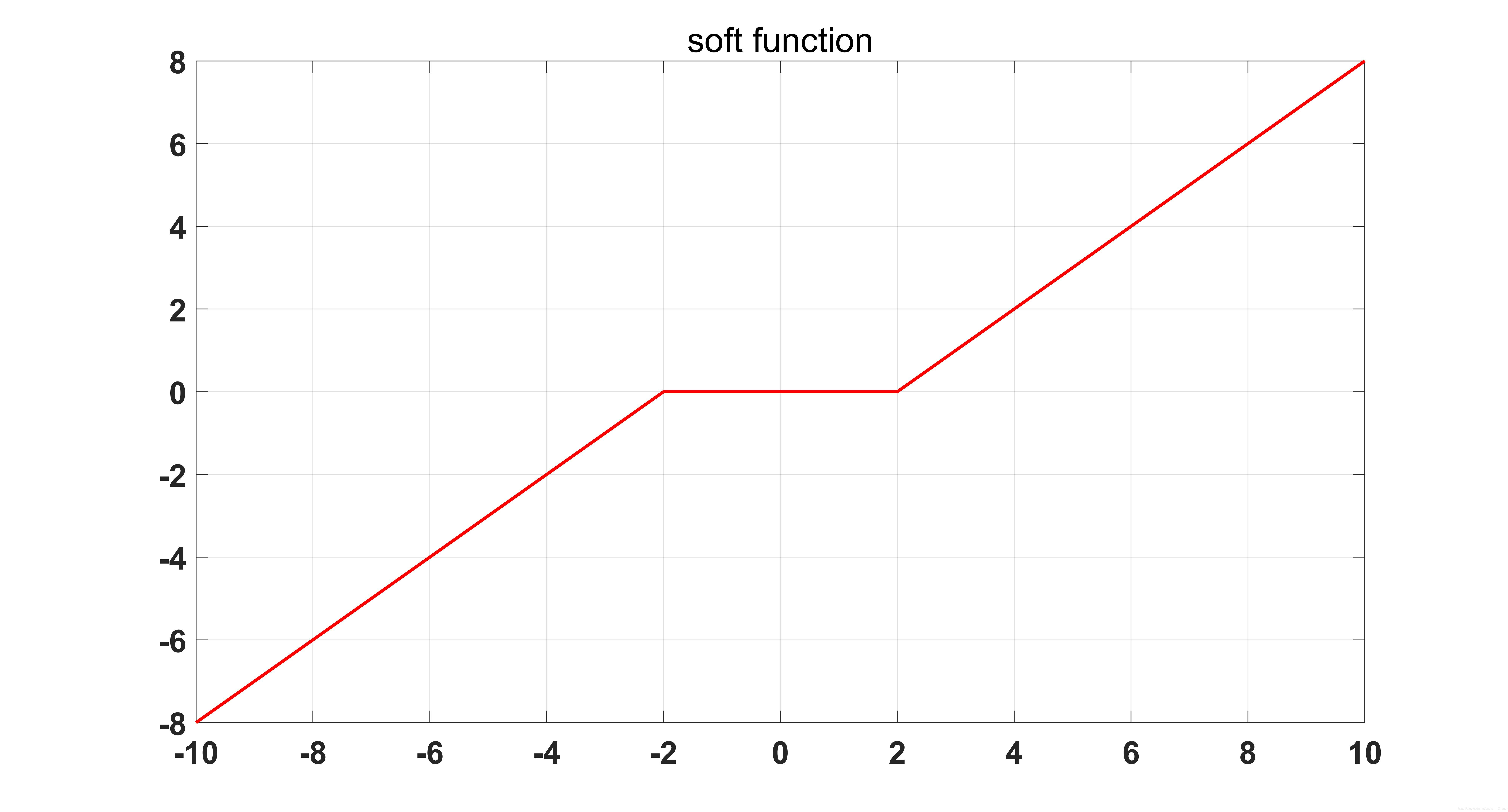
如果令 $W=-B^TB$,那么就有
$$
x_{t+1} = P_{\mu_tλ} \bigg((I_n + \mu W)x_t + \mu_tB^T y\bigg) ,
$$
于是作者认为, $(I_n + \mu W)$ 就是自身映射,而 $\mu_tB^T y$ 则可以看作是初始层残差连接。另外 $P_β(·)$ 的作用可以类比为 GCNII 的非线性函数,如 $ReLU$。作者的想法也很可能是从该算法上得到的启发。
另外,作者还提出了 GCNII 的一个变式 GCNII*,公式如下。主要区别在于,他对初始化层也乘上了一个带自身映射的参数矩阵。
$$
H^{(l+1)} =\sigma\bigg((1−\alpha_l) \tilde PH^{(l)} \bigg( (1−\beta_l)I_n +\beta_l W^{(l)}_1 \bigg)+\alpha_l H^{(0)}\bigg( (1−\beta_l)I_n +\beta_l W^{(l)}_2 \bigg)\bigg)
$$
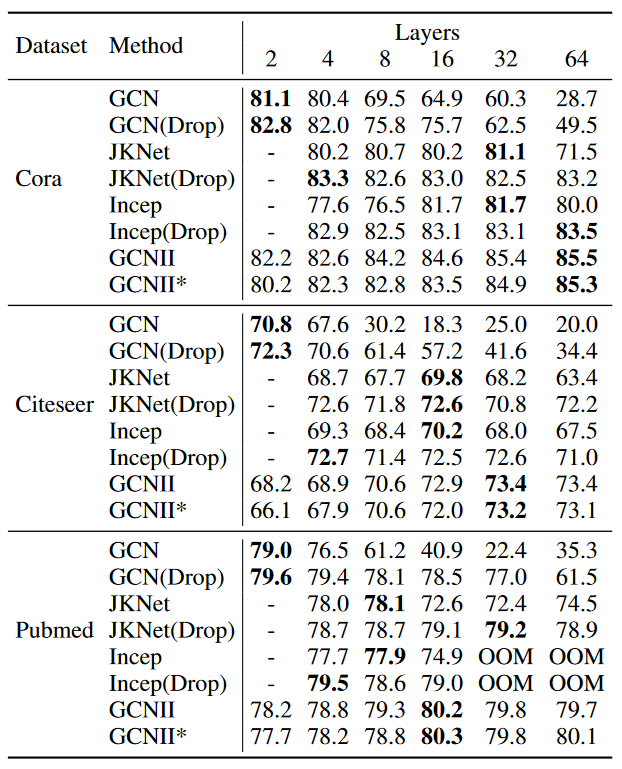
根据最后的结果,可以看到 GCN 和 GCNII 即便在高达64层的深度,性能也并未有明显减弱,甚至会达到较高的水准。但值得一提的是,表格中没有展现 APPNP 的性能,事实上 APPNP 的性能也是有如此特点的。
Spectral Aanlaysis
作者首先分析了带残差连接的 GCN,其最后也是会收敛到一个值,$π = \frac{\langle \tilde{D}^{1/2} 1,x\rangle} {2m+n}$。
作者对每一层的结点做了分析,最后得到对于第 $K$ 层的 $j$ 结点有:
$$
h^{(K)}(j)=\sqrt{d_j+1}\bigg(\sum_{i=1}^{n}\frac{\sqrt{d_i+1}}{2m+n}x_i\pm\frac{\sum_{i=1}^nx_i\big(1-\frac{\lambda_\tilde{G}^2}{2}\big)^K}{\sqrt{d_j+1}}\bigg)
$$
其中,$\lambda_\tilde{G}$ 带自环的规范化拉普拉斯矩阵的 $\tilde L = I_n − \tilde{D}^{−1/2} \tilde{A} \tilde{D}^{−1/2}$ 的最小非0特征值,$m,n$ 分别为结点和边的数量。可以看到,对于结点 $j$ 来说,如果有更大的度数 $d_j$,那么就有更大的 $\sqrt{d_j + 1}$,其收敛到终态的速度也就越快(注意 $\pm$ 后一项会趋向于0)。
作者也从 Spectral 的角度分析了 GCNII,作者认为,一个 K 层的 GCNII,他可以模拟以下多项式:
$$
\sum^{K}_{l=0}\theta_l\tilde{L}^{l}
$$
且参数 $\theta$ 是 arbitrary 的。这个形式在 [[Notes for Collection 1#ChebNet|GCN]] 中就有提及,但需注意的是,作者认为 GCN 中的 $\theta$ 是 fixed 的[[[WHY]]]。我对这里的 fixed 和 arbitrary 不是很理解。个人感觉,大概是说对于 GCN 来说,对于某个任务他最后学得的最优参数只有一种可能,但是对于 GCNII 来说,可以用过调节 $\alpha$ 和 $\beta$ 来获得任意可能的解。
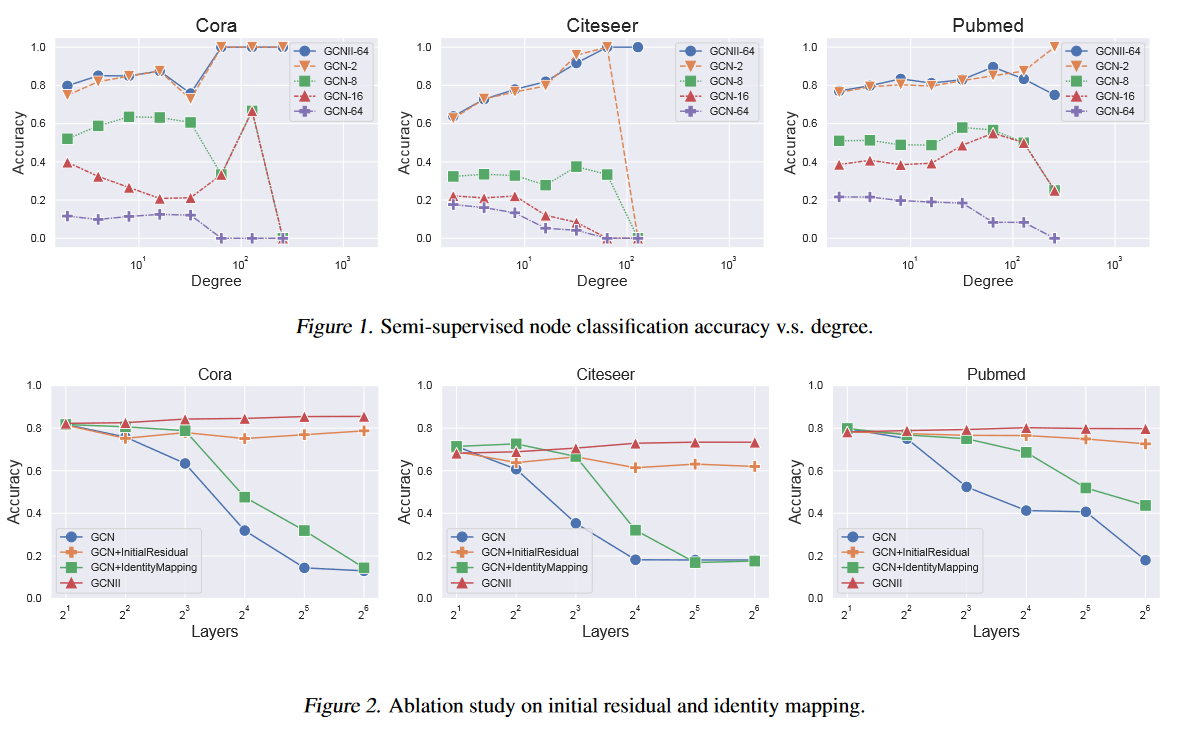
作者也做了实验的验证。首先结点度数对 GNN 的影响。作者根据结点的根据度数的范围 $[2^i, 2^{i+1})$ , $i = 0, . . . , \infty$,分成了一个个组。并分别计算各个组的准确率。得到上图中的 figure 1。可以看到,对于度数会越高的组别,其准确率下降的越厉害。尤其在 Cora 和 Citeseer 度数 100 之后,甚至连 GCN-2(residual) 准确率降至0。
此外作者还做了消融实验,验证了添加的2个模块的有效性。但从图中也可以看出,虽然 GCN 做不深,但浅层的 GCN 效果也不错,而做深的 GCNII 其实并没有好太多,不得不怀疑做深是否有必要。
Limitation
文章聚焦于把网络做深,但是做深的效果并没有好太多。这种深度加大的行为,性价比可能并不高。
Conclusion
作者通过加入初始化残差和自身映射,引入2个超参数调节模型,确实能把网络做的很深,不至于梯度消失、过拟合或者说Oversmoothing,其效果也略有上升,但是其性能的调高很有限。不过在大模型时代,不顾一切地把网络做深也许确实能够带来性能的极大提升,这或许也是为什么这么多论文想把 GNN 做深的原因了。
DeeperGCN All You Need to Train Deeper GCNs
Massage Passing
论文将 GNN 抽象成了3个阶段:1. Message Construction,2. Message Aggregation,3. Vertex Update。
这在 PyG 中,有着同样的分类。具体参考 *Creating Message Passing Networks*。公式可描述如下:
$$
\mathbf{x}_i^{(k)} = \gamma^{(k)} \left( \mathbf{x}i^{(k-1)}, \bigoplus{j \in \mathcal{N}(i)} , \phi^{(k)}\left(\mathbf{x}_i^{(k-1)}, \mathbf{x}j^{(k-1)},\mathbf{e}{j,i}\right) \right),
$$
其中 $\phi,\bigoplus, \gamma$ 分别表示1、2、3这3个阶段。其中,$\bigoplus$ 是一个 Permutation Invariant 的函数,而 $\phi_k,\gamma$ 往往是一个可微函数,比如MLP。
后2个阶段是常用的,但是第1个阶段,可能并未明确点出。其实,在 GCN 中,我可以将对结点特征做 Normalize 作为 Message Construction。即所有的 Message 是带权重的特征,且权重为 $1/\sqrt{d_id_j}$。因此 $\phi$ 函数的输入需要输入结点可能需要源节点和邻居结点以及他们的边信息。
另外,在之前大部分论文中,遇到的数据集边是没有特征的,如果边存在特征,那 Message 该如何构建呢?这里提供一种论文使用的办法。
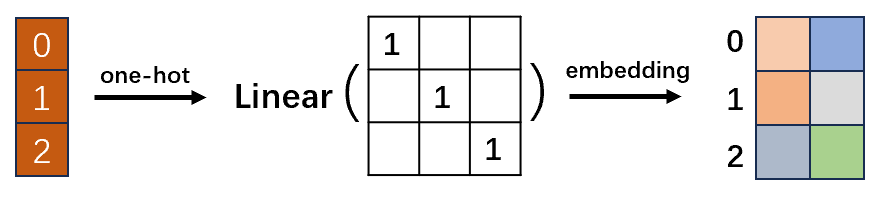
首先,我们在对离散数据编码时,往往常用 one-hot 编码,比如在 NLP 中,在语料库中存在 N 个 Token,那就编码为 N 维的 one-hot 向量。但是 one-hot 向量有时候因为过度稀疏、维度过大,并且无法表示各个向量之间的关系,比如相近语义的词语在向量表示时应当给予更接近的距离,而非 one-hot 中,所有向量都是单位正交的。所以,有一种常用的方法,就是利用线性变换,即乘上一个参数矩阵,来对每一词语重新编码,这个过程叫做 embedding。经过这样的 embedding,每一个词语会获得新的表示想浪。如上图所示,将每一个特征值都从原来的3维向量编码成了2维向量。
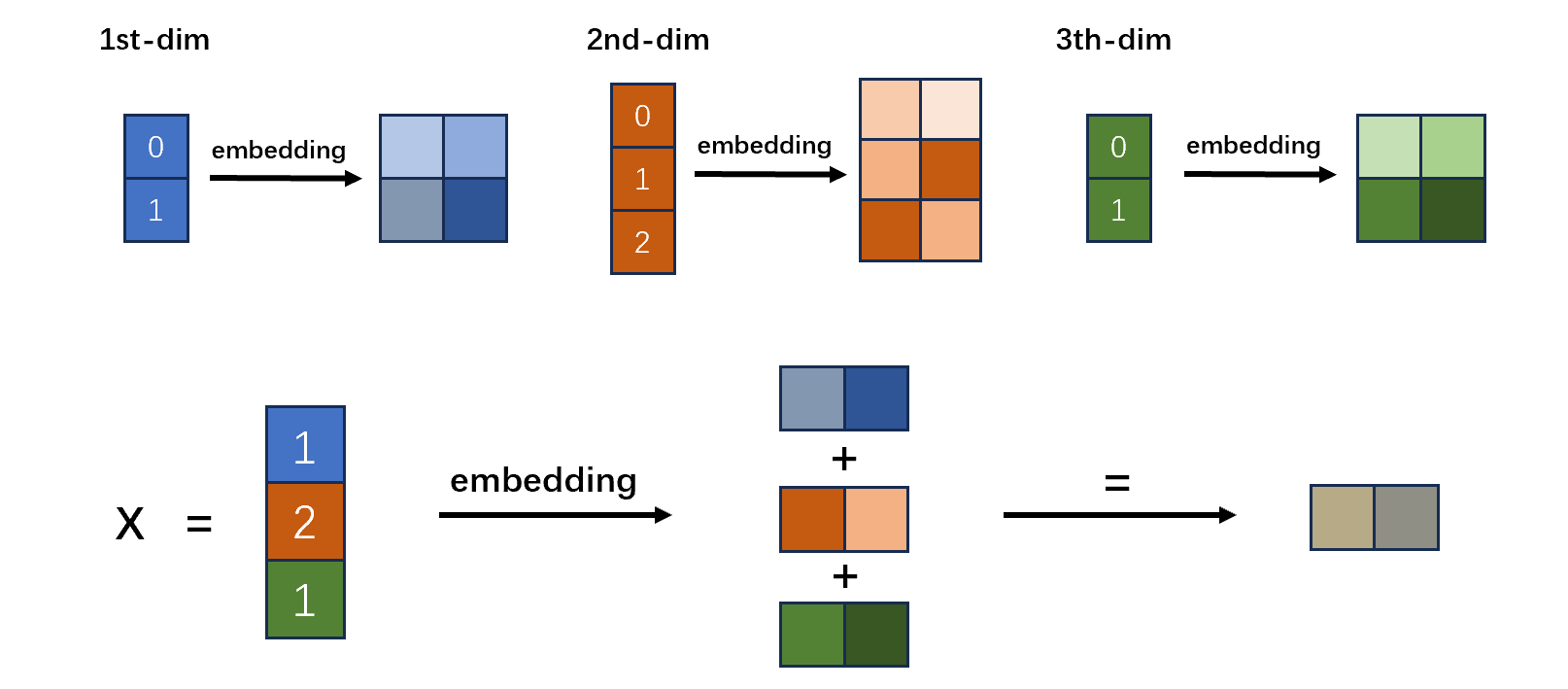
而在很多图任务中,结点特征以及边特征的每一维取值也是离散的,也就是说特征的每一维都可以进行 ont-hot 编码,比如结点的第一维特征可能取值是0和1,那么它可以编码为 $2 \times 2$ 的 one-hot 矩阵,同时也可以将其做一个 embedding 的操作。那么我们对特征的每一维都可以做相同的操作,将每一维的特征的每一个取值都编码成相同维度的向量。如上图所示,假设输入特征,第一维有2种取值,第2维有3种取值,第3维有2种取值。对每一维的特征都做一个 embedding,使得每一维的特征的每一个特征取值都对应到一个维度为2的 embedding 向量。那么最后输入的特征,根据每一维的特征取值,将对应的 embedding 向量取出相加,就是最后的特征向量了。
这样的操作,同时作用在结点特征和边特征上,使他们最后的 embedding 向量维度保持一致,这样就能更容易进行特征融合,比如把边的特征加到结点特征上,得到最终的 message。
需要注意的是,在做 embedding 的时候,也就是做了一个线性变换,但变换的参数矩阵中的参数是不知道的,有的可能会使用通过一些手段预训练的参数。但总之,一般会跟随整个模型一起训练。
Generalized Aggregator
该文的一个核心内容就是作者提出了一个通用的信息聚合器。我们知道,常用的聚合器有mean, max, sum等。作者提出了2个可以根据参数连续变化的聚合器,并且它的变化范围是mean ~ max之间。但其中并不包含 sum,作者说 sum 容易被包括,但事实上他在附录中将其作为 Future Work。
首先是 Softmax 聚合器的公式如下:
$$
\operatorname{SoftMax_Agg}{\beta}(\cdot)=\sum{u\in \mathcal{N}(v)}\frac{\exp(\beta \mathbf{m}{vu})}{\sum{i\in \mathcal{N}(v)}\exp(\beta\mathbf{m}{vi})}\cdot \mathbf{m}{vu}
$$
其中,$m_{vu}$ 为 message。不过这里需要注意的是,以上是论文的形式,但在代码中发现一些区别,具体参考 *[[Code for Collection 2#SoftMax - Max Firstly|SoftMax - Max Firstly]]*。
可以发现,当 $\beta =0$ 时,它是 mean,$\beta \rightarrow +\infty$ 时,它是 max(直观的理解就是,当趋向于无穷时,最大的数和其他数的差距拉到了无穷大,所以只有最大数前的系数趋向于1,其余为0)。
此外,作者还提出了 PowerMean 聚合器:
$$
\operatorname{Power_Agg}(\cdot)=\bigg(\frac{1}{|\mathcal{N}(v)}\sum_{u\in\mathcal{N}{v}}\mathbf{m}^{p}_{vu}\bigg)^{\frac{1}{p}}
$$
这里 $p$ 是个非0值,当 $p =1$ 时,它是 mean,$p \rightarrow +\infty$ 时,它是 max,且当 $p=-1$ 时是几何均值,当 $p\rightarrow 0$ 是调和均值。具体可参考 *PowerMean*。
值得注意的是,PowerMean 聚合器的特征值不能为0。实际上的实现,也和公式的表示略有区别,具体可参考 *[[Code for Collection 2#PowerMean - Clamp Firstly|PowerMean - Clamp Firstly]]*。
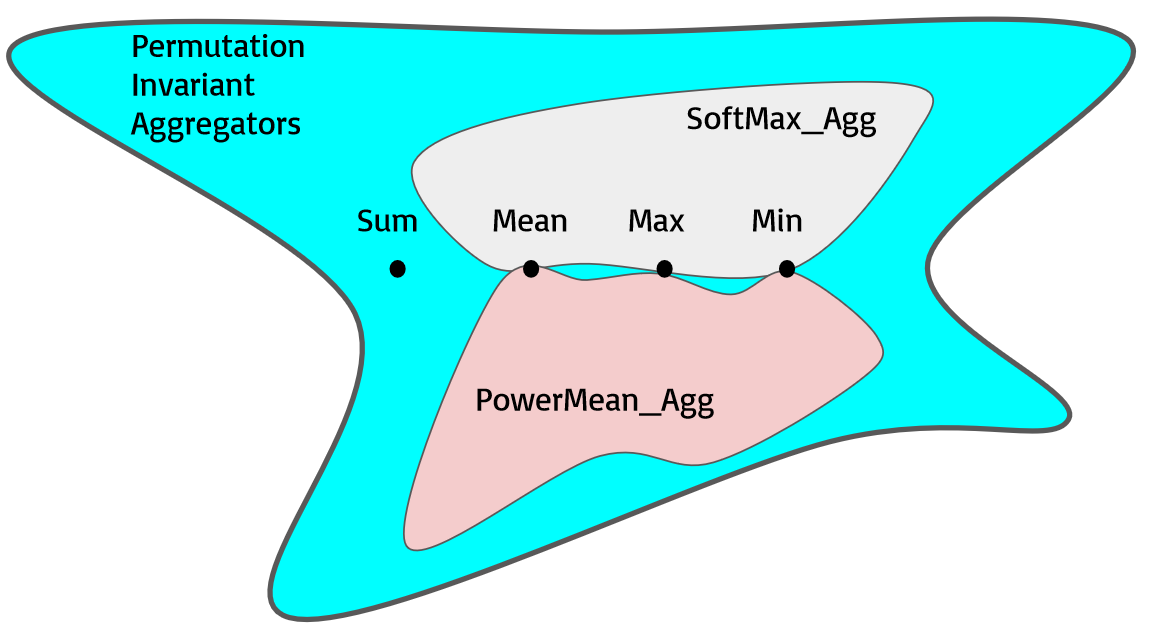
另外作者认为,作者用以上的图来表示它所提出的聚合器所覆盖的范围。按照上图所示,SoftMax 和 PowerMean 仅有 Mean,Max 和 Min 的交集[[[WHY]]]。
另外,作者还尝试将这2个聚合器往 sum 上靠,然后它提出了以下的聚合器形式:
$$
∣\mathcal{N}(v)∣^y \cdot \operatorname{Agg}(\cdot)
$$
他发现,当 $y=1$,且 Agg 为 Mean 时,聚合器为 Sum。另外,在他实现的代码中,也做了进一步的调整,具体可参考 [[Code for Collection 2#How to get Sum|How to get Sum]].
GENeralized Aggregation Networks (GEN)
论文中,作者提出了一个新的消息传播(Message Passing)模型,或者也可将其看作是神经网络中的一个 Layer,并命名为 GEN。
第一步是 Message Construction,正如在 [[#Massage Passing|Message Passing]] 一节中所说,作者的 Message Passing,先通过了 embedding,然后
$$
\mathbf m^{(l)}{vu} = \rho^{(l)}(\mathbf h^{(l)}v , \mathbf h^{(l)}u , \mathbf h^{(l)}{e{vu}} ) = \operatorname{ReLU}(\mathbf h^{(l)}u + \mathbb{1}(\mathbf h^{(l)} {e{vu}} ) \cdot (\mathbf h^{(l)}{e{vu}} ) + \epsilon, u \in \mathcal{N} (v)
$$
第二步是 Message Aggregation,也就是进行消息传播,使用的聚合器可以是普通的 Mean/Sum/Max,同样可以设置为在该论文中提出的新型聚合器:Softamax、PowerMean。
第三步是 Vertex Update,作者首先对特征进行了 Normalization,再将其通过 MLP。其公式如下。其中 $s$ 是一个可学习的参数(作者也比较了采用固定参数对性能的影响,结果说明效果和聚合器有关,整体上使用可学习参数更好)。注意这里的 $\mathbf h_v$ 指的是经过第一步前的表示向量,而 $\mathbf m_v$ 则是经过第二步后的表示向量。
$$
\mathbf h^{(l+1)}_v = \phi^{(l)}(\mathbf h^{(l)}_v , \mathbf m^{(l)}_v ) = \operatorname{MLP}(\mathbf h^{(l)}_v + s\cdot\Vert \mathbf h^{(l)}_v\Vert_2 \cdot \frac{\mathbf m^{(l)}_v }{\Vert \mathbf m^{(l)}_v \Vert_2 })
$$
那么以上就是作者提出的整个 GEN Layer了。
另外作者还认为 Normalization (BatchNorm/LayerNorm) 拜访位置也会影响性能,他认为 Norm -> ReLU -> GEN 可以带来更好的性能。
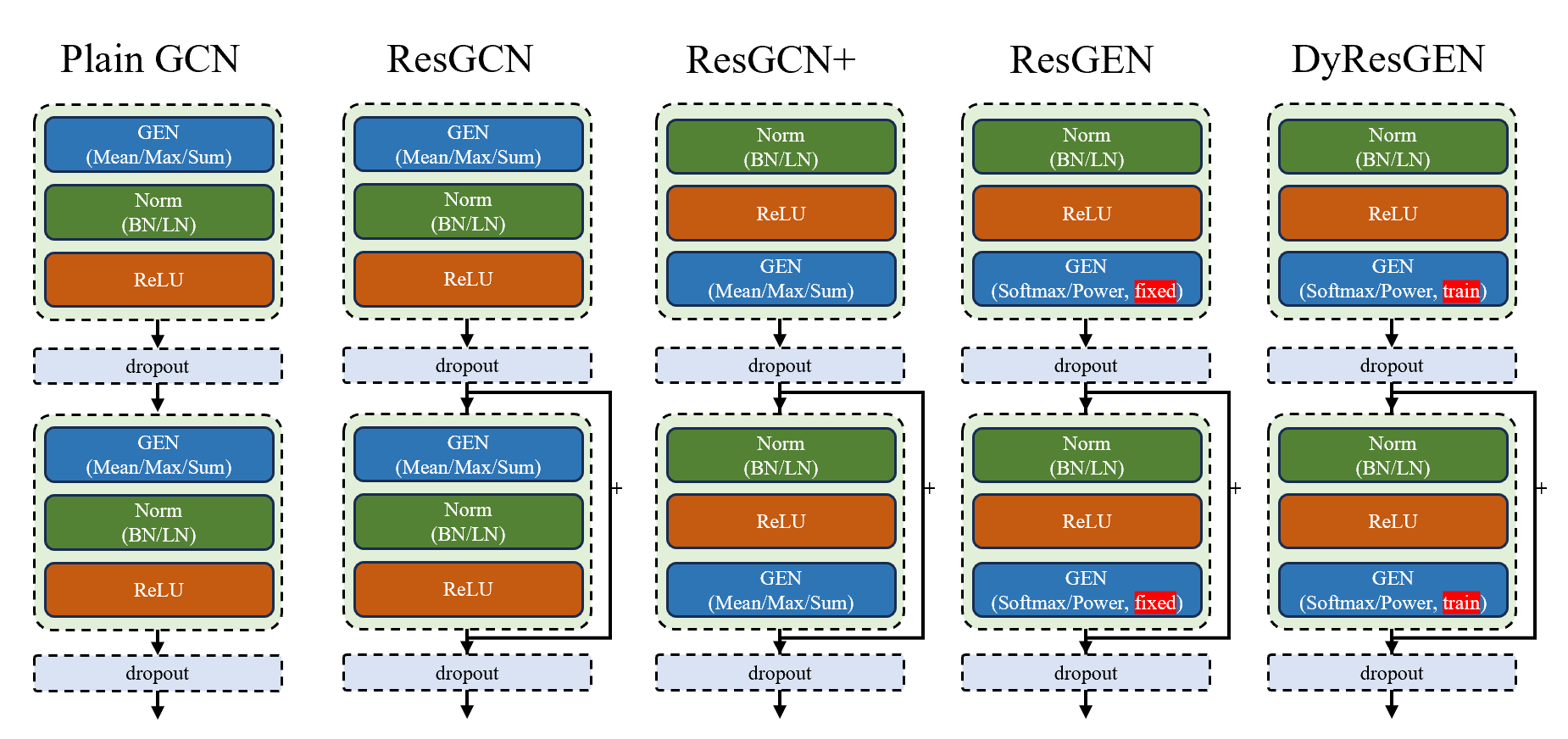
接着作者将 GEN Layer 和其他结构混合,提出了5个模型,如上图所示。可以看到,主要的区别在于 Normalization (BatchNorm/LayerNorm) 以及 ReLU 的位置不同、是否有残差连接、使用的聚合器是否为论文提出的SoftMax和PowerMean、聚合器的参数是固定的还是可学习的。
通过这种组合方式,旨在说明每一个变化是否能够提高性能。那么这里要说的是,哪些属于作者的模型。某种程度了上来说都属于。就算是 Plain GCN,它使用的 GEN 采用的是 Mean / Max / Sum 这类朴素的聚合器,但 GEN 中第一步的 Message Construction 和第三步的 Vertex Update 的方式都和其他模型有所不同,因此只要这 5 个模型有一个性能高即可。另外这 5 个模型并不一定是进化的关系,可以将其视作是模型的超参数。
Limitation
对于聚合器中 $p$ 和 $\beta$ 参数,他们的变化范围最大可以到正无穷,即无边界。这是非常不好的,因为最佳参数可能造成计算溢出。
Conclusion
本文的核心主要有以下几点:
- 提出了新的 Message Passing 的模型(或者 Layer):GEN,它包含
- 新的 Message Construction 的方式
- 新的聚合器,SoftMax 和 PowerMean,他们可以在 Mean 和 Max 聚合器中连续变化
- 新的 Vertex Update 的方式,即引入了 Message Normalization
- 提出了新的 Normalization (BatchNorm / LayerNorm) 的摆放位置
- 将以上 2 点和残差连接相互组合,得到5个不同的模型。
GRAND Graph Random Neural Networks for Semi-Supervised Learning on Graphs
Drop Nodes and Random Propagation
第一步:和 [[#DropEdge Towards Deep Graph Convolutional Networks On Node Classification|DropEdge]] 的想法相似,该论文采用 Drop Nodes 的方法来增强原数据集。也就是说,每个结点特征 $x$ 将以概率 $p$ 随机置0,由于采样符合伯努利分布,为了使数据的期望和原数据保持一致,我们会再乘上因子 $\frac{1}{1-p}$。这一操作事实上在 dropout 中是默认的,可参考 pytorch 文档 *dropout*。但是要注意 Drop Nodes 是将某一结点的特征全置为0,而 Dropout 是将特征矩阵中的某一元素置为0,其细粒度不同。
第二步:DropNode 之后,作者提出了另一个操作 Random Propagation。事实上就是将 0 到 K 阶的传播矩阵求个平均值,最后和特征矩阵相乘,这个操作没什么新奇的,它可以比较大程度地保留临近结点的特征。
第三步:结束以上2个操作后,将其输入到 MLP 预测。
以上过程可以用如下公式表示:
$$
\begin{align}
M =& \operatorname{drop}(\mathbf{1},p)\times \mathbf{1}^T\
% &符号要放在等号后面??
\widetilde{X} =& \frac{M\cdot X}{1-p} \tag{Drop Nodes}\
\overline{A}^{(s)} =& \frac{1}{s+1}\sum_{i=0}^s \hat A^i\
\overline{X}^{(s)} =& \overline{A}^{(s)}\widetilde{X}\tag{Random Propagation}\
\widetilde{Z}^{(s)} =& \operatorname{MLP}(\overline{X},\Theta) \tag{Prediction}
\end{align}
$$
其中 Drop Nodes 可以首先获取一个 0/1 的 mask,在让 mask 和原数据相乘。 $M$ 为 Mask,$\operatorname{drop}(\cdot,p)$ 就是以 $p$ 的概率将元素随机置 0 的操作,$\mathbf{1}\in \mathbb{R}^{N\times 1}$ 是一个全 1 向量,输入的特征矩阵 $X\in \mathbb{R}^{N\times F}$, $\hat A$ 为传播矩阵。
值得注意的是,以上公式中,假设总共传播 $S$ 次,那么可以得到 $S$ 个预测结果。
Sharpening and Regularization
从前面一小节得到的 $S$ 个预测结果后,在经过以下的求均值和 sharpening 的操作。
$$
\begin{align}
\overline{Z}&=\frac{1}{S}\sum_{s=1}^{S}\widetilde Z^{(s)}\
\overline{Z}{ij}’&= \overline{Z}^{\frac{1}{T}}{ij}\bigg/\sum_{c=0}^{C-1}\overline{Z}_{ic}^{\frac{1}{T}},(j=0,1,…,C-1)
\end{align}
$$
求均值是好理解的,但是可能对 sharpening 不是很能理解。该操作可以让原来的概率分布更极端化,使小的更小,大的更大,尤其当 $T\rightarrow \infty$ 时,对于每个结点对应的预测将是一个 one-hot 向量。我猜测是因为上述求均值的原因,平滑化了结点预测的概率分布,不利于优化,并且得到的分类器也是不合理的。需要注意的是 $T$ 是个超参数。
那么最后在训练时有 2 个损失,1个是各个 $\widetilde Z^{(s)}$ 和真实标签的交叉熵损失,还有一个则是各个预测如 $\widetilde{Z}^{(s_1)}$ 和 $\widetilde{Z}^{(s_2)}$ 的距离,我们成为一致性 (Consistency) 损失,即我们希望各个层次的预测应当不能相差太多,要尽量的接近。后一项损失我们可以看作是一个正则化项。总的损失可表示为如下公式。
$$
\begin{align}
\mathcal{L}{con} &= \frac{1}{S}\sum{s=1}^{S}\sum_{i=0}^{m-1} Y^T_i \log\widetilde{Z}i^{(s)}\
\mathcal{L}{con} &= \frac{1}{S}\sum_{s=1}^{S}\sum_{i=0}^{n-1}\Vert \overline{Z}{i}’-\widetilde{Z}^{(x)}i \Vert_2^2\
\mathcal{L} &= \mathcal{L}{sup} + \lambda\mathcal{L}{con}\
\end{align}
$$
GRAND
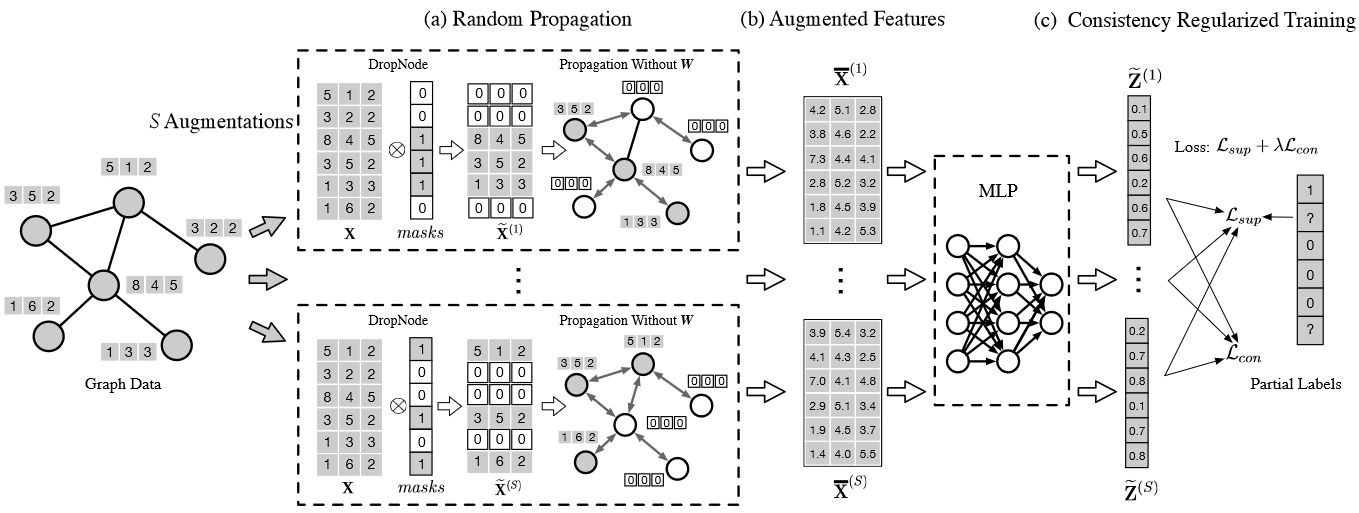
最后我们在整体看一下论文提出的模型,它可以用以上的图来表示,尤其是 DropNode 一块表现的是比较清晰的。
但更具体的,还可以用如下的伪代码来表示

Three Issues
该论文从开始就提出了 GCN 广泛存在的 3 个问题:1. 过拟合;2. 鲁棒性差;3. 过度平滑。
我们来看一下该模型是否有一定程度上缓解了这些问题。
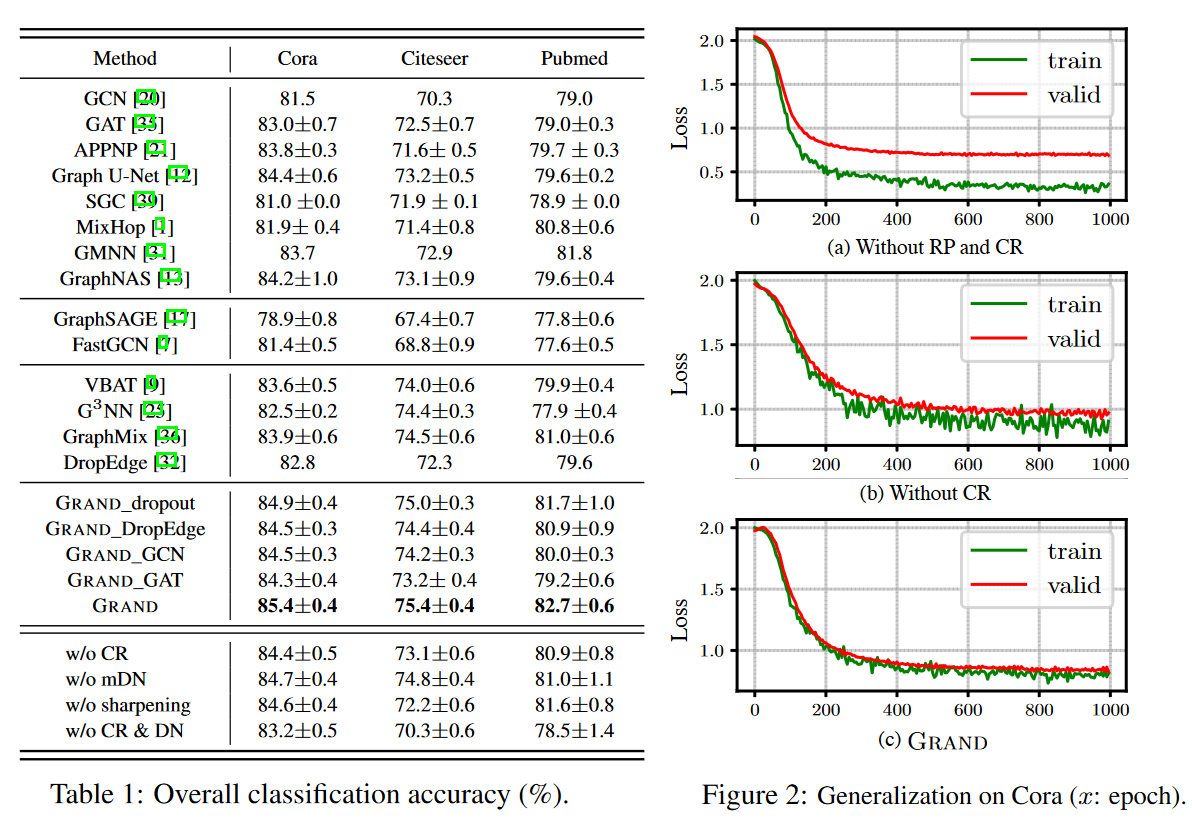
首先是过拟合,也就是模型的泛化能力(generalization),上图中的 Figure 2 表现了不同模型训练损失和验证集损失的关系,可以看到 GRAND 模型在添加了 RP(Random Propagation) 和 CR(Consistency Regularization)模块后,训练损失和验证集损失是比较接近的。
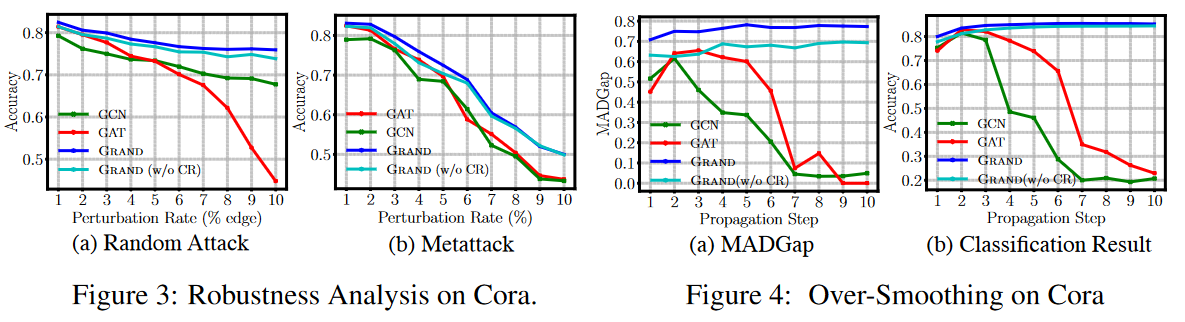
另外我们再来看一下鲁棒性,作者通过往数据集中随机增加伪边,以及基于元学习[[[WHAT]]]的增减边来对原数据集进行破坏,从 Figure 3 可以看出 GAT 对破坏后的数据集是比较敏感的,而GRAND展现出比较优良的性能。
Limitation
关于缺陷,在论文中也有提到,GRAND 是基于同配性假设的,即物以类聚。假如图缺乏同配性,即相似的结点并没有相互连接,那么效果可能会不好。这是很多半监督学习以及图神经网络共同的缺陷。
Conclusion
作者的模型可以归为2个技术,一个是数据增强技术,即作者所谓的 Drop Nodes 和 Random Propagation,另一个则是正则化技术,通过让多种预测结果尽量接近,而制定正则化项。作者也确实一定程度上缓解了它提出的3个问题。
附录
Vapnik–Chervonenkis dimension
- Y. Rong, W. Huang, T. Xu, and J. Huang, “DropEdge: Towards Deep Graph Convolutional Networks on Node Classification.” arXiv, Mar. 12, 2020. doi: 10.48550/arXiv.1907.10903. ↩
- Q. Li, Z. Han, and X.-M. Wu, “Deeper insights into graph convolutional networks for semi-supervised learning,” in Proceedings of the AAAI conference on artificial intelligence, 2018. ↩
- A. Fout, J. Byrd, B. Shariat, and A. Ben-Hur, “Protein Interface Prediction using Graph Convolutional Networks,” in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017. Accessed: Aug. 06, 2023. [Online]. Available:https://proceedings.neurips.cc/paper_files/paper/2017/hash/f507783927f2ec2737ba40afbd17efb5-Abstract.html ↩
- T. Hastie, S. Rosset, J. Zhu, and H. Zou, “Multi-class AdaBoost,” Stat. Interface, vol. 2, no. 3, pp. 349–360, 2009, doi: 10.4310/SII.2009.v2.n3.a8. ↩
- M. Hardt and T. Ma, “Identity Matters in Deep Learning.” arXiv, Jul. 20, 2018. doi: 10.48550/arXiv.1611.04231. ↩