论文速读<二>：GNN系列

论文速读系列的第二期，论文速读主要提取论文的Key Idea，本期为GNN系列的论文速读，选取了4篇经典论文和3篇近期的论文。上期为知识图谱领域的关系抽取。

Key Idea

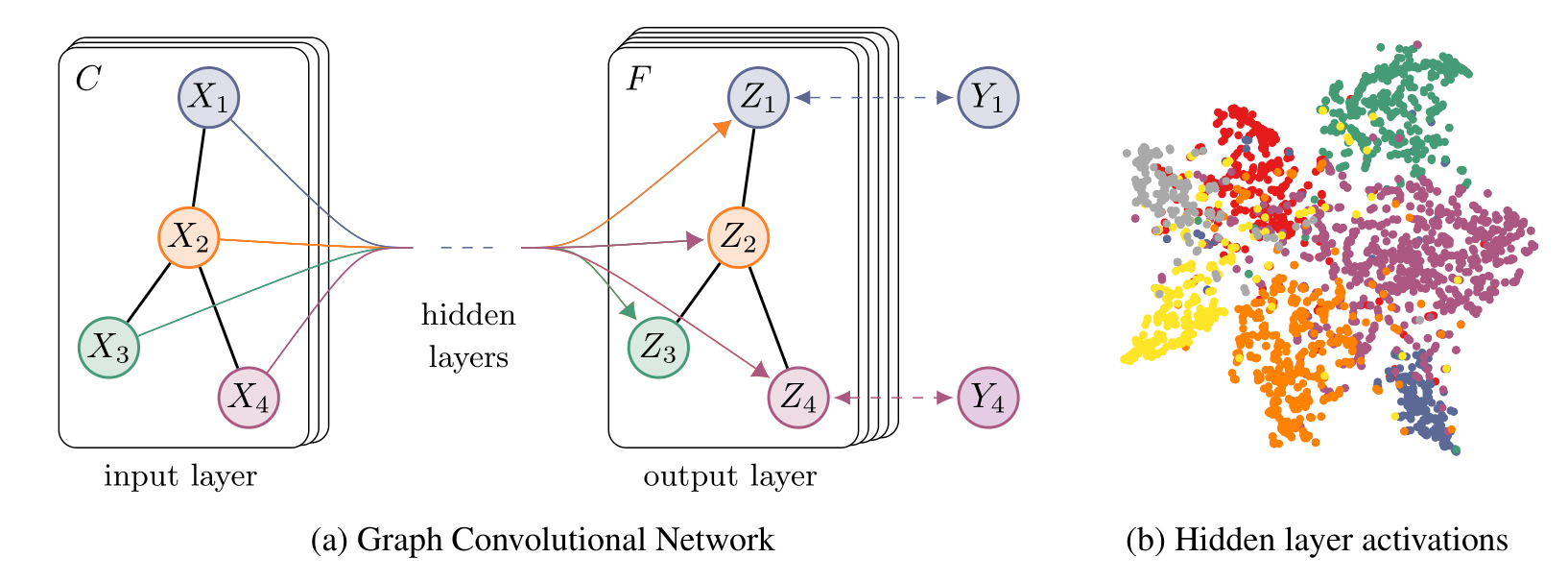
Semi-supervised Classification with Graph Convolutional Networks^[1]

GCN的核心公式如下，其中\(\sigma\)表示激活函数，\(\tilde A=A+I\)，也就是给每个结点加个自环，\(\tilde D=\sum_i A_{ij}\)。\(H^{(l)}\)为第\(l\)层的embedding，\(W\)是参数矩阵。它的形式看起来非常简单。 \[ H^{(l+1)}=\sigma (\tilde D^{-\frac{1}{2}}\tilde A\tilde D^{-\frac{1}{2}}H^{(l)}W^{(l)}) \] 从卷积的参数共享角度来看，其实就是每个结点的将自己与附近的参数聚合。第1次聚合后每个结点获取了直接邻居结点的特征，但第2次聚合就可以获取间接邻居的特征（因为直接邻居包含了它的邻居的特征）。所以在多层聚合下，每个结点可以获得全局的信息。

Graph Attention Networks^[2]

GAN就是在GNN中加入注意力机制

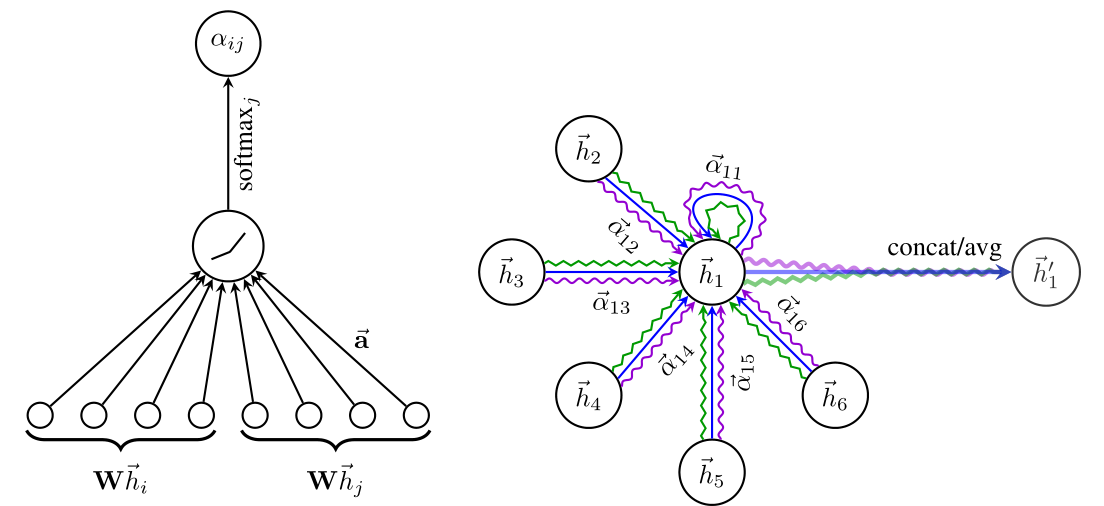
以下是注意力的计算公式，其中\(\vec h_i,shape(F,1);W,shape(F',F);\vec a,shape(2F',1)\)。\(||\)表示连接。看起来就是对2个向量进行线性变换后连接，再通过\(\vec a\)他们获取之间的相关性，再做一个归一化。

\[ \alpha_{ij}=\frac{\exp(LeakyReLU(\vec a^T[W\vec h_i|| W\vec h_j]))}{\sum_{k\in N_i}\exp(LeakyReLU(\vec a^T[W\vec h_i||W\vec h_j]))} \] 和普通神经网络的注意力机制相同，GAN中也分为多头和单头的注意力机制。

\(\vec h_i\)的更新，单头注意力 \[ \vec h'_i = \sigma(\sum_{j\in N_i} \alpha_{ij}W\vec h^i) \] 2种多头注意力的实现 \[ \vec h'_i = ||^{K}_{k=1} \sigma(\sum_{j\in N_i} \alpha^k_{ij}W^k\vec h^i)\\ \vec h'_i = \sigma(\frac{1}{K}\sum^{K}_{k=1}\sum_{j\in N_i} \alpha^k_{ij}W^k\vec h^i) \]

How Powerful are Graph Neural Networks?^[3]

这篇文章理论方面证明了GNN的上限是WL test(图同构测试)的上接，总结了信息聚合的方法以及对GNN的评价指标。 \[ h_{k+1}(u) = MLP((1+\epsilon) h_k(u) + \sum_{(u,v) \in E} h_k(v)) \] 其中\(\epsilon\)是一个可学习的无理数参数。该论证证明了其可以达到WL test的上界。

Inductive Representation Learning on Large Graphs^[4]

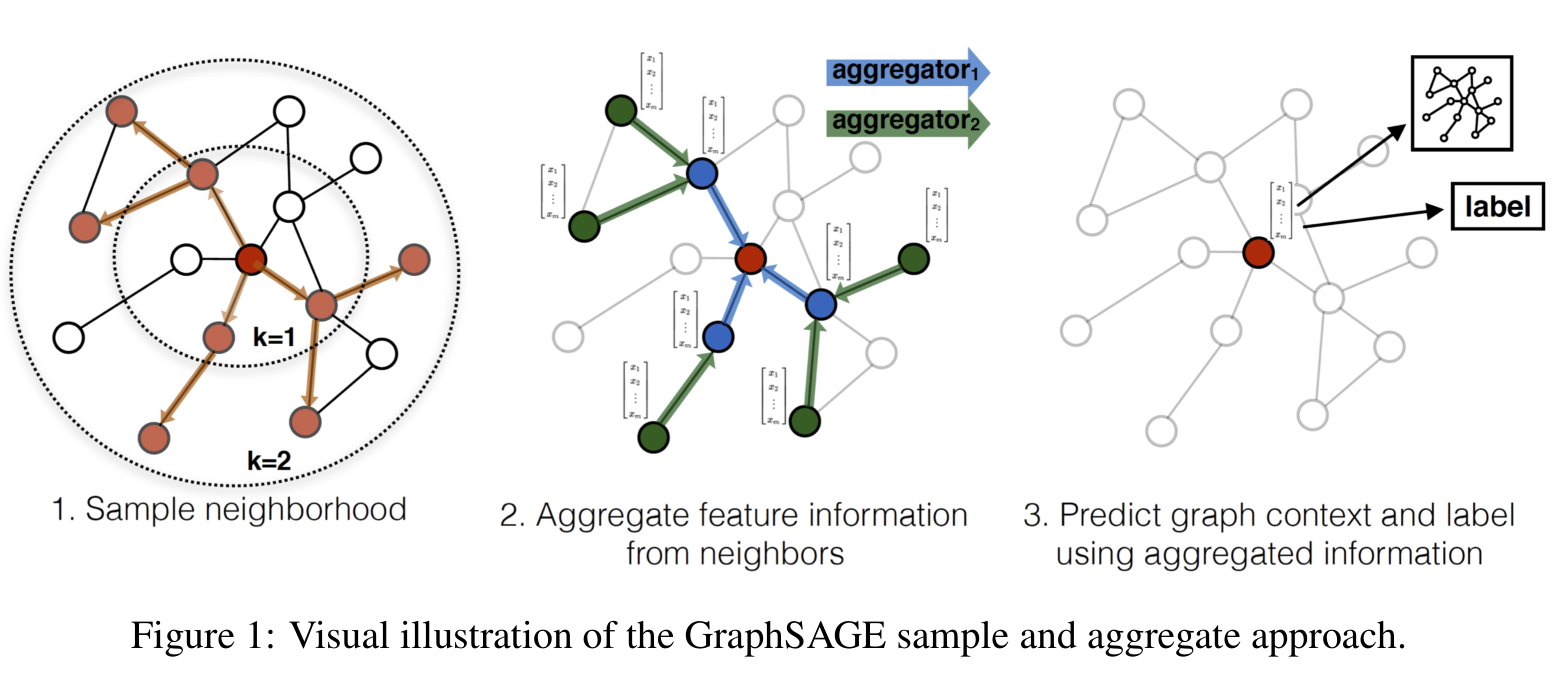
如上图所示，GraphSAGE可以分为3个步骤：1. 对图中每个顶点邻居顶点进行采样；2. 根据聚合函数聚合邻居顶点蕴含的信息；3. 得到图中各顶点的向量表示供下游任务使用。

每层的embedding生成可以用如上图的伪代码表示。其中AGGREGATE可以使用均值、池化以及LSTM函数。

Finding Global Homophily in Graph Neural Networks When Meeting Heterophily^[5]

全局同质性、异质图。现有的网络通过多次的领域聚合获取远距离的信息。本文通过相关系数矩阵（类似于注意力机制）获取全局信息。且相关系数矩阵可转换为有闭式解的优化问题，经过简化，可将计算复杂度缩小至线性。

GloGNN，GloGNN++（系数矩阵加上了自相关）。

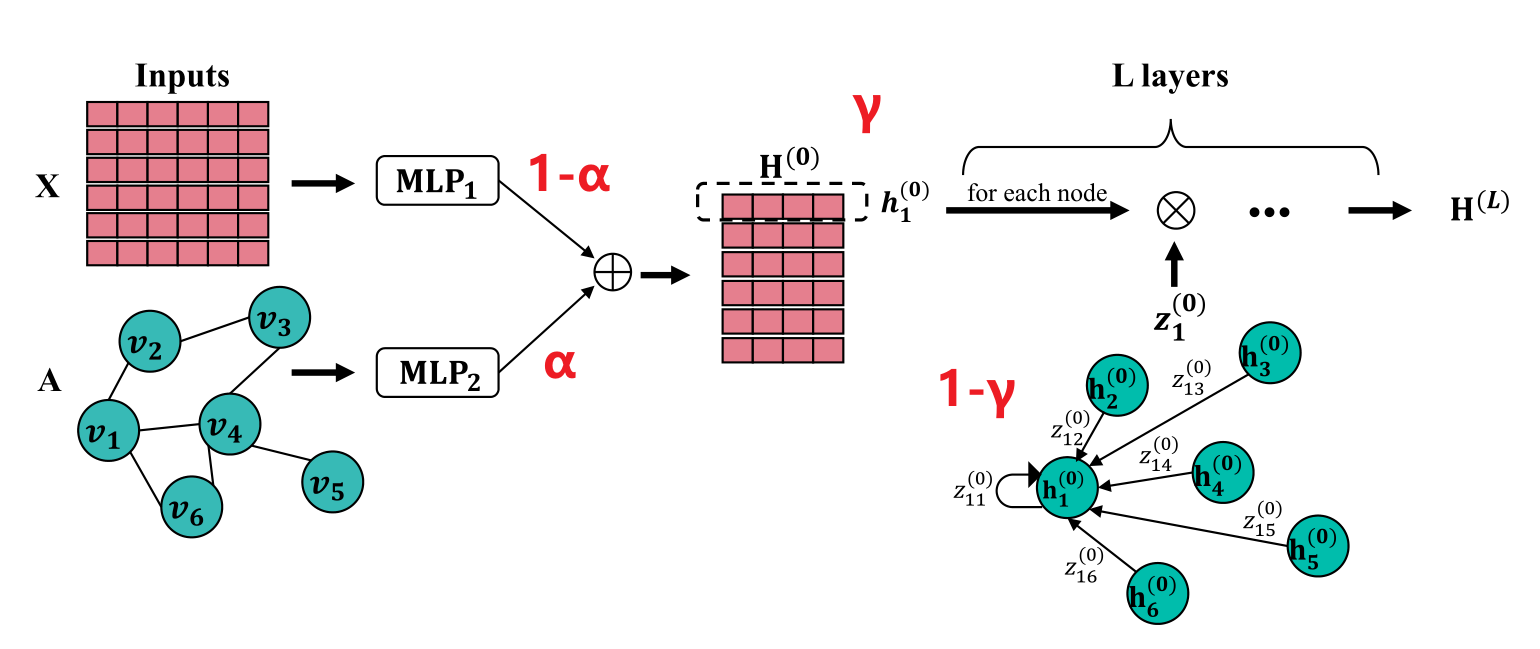
核心公式 \[ H^{(0)}=(1-\alpha)MLP_1(X)+\alpha MLP_2(A)\\ H^{(l+1)}=(1-\gamma)Z^{(l)*}H^{(l)}+\gamma H^{(0)}\\ \] \(Z^{(l)*}\)通过求解优化问题的闭式解获得。

Grouping Effect：通过证明可得，\(Z^{(l*)},(Z^{(l*)})^T,H^{(l+1)}\)都具有grouping effect。即当特征足够接近、结构足够接近时，对应结点的特征表示也足够接近，相关系数也足够接近。

Large Scale Learning on Non-Homophilous Graphs: New Benchmarks and Strong Simple Methods^[6]

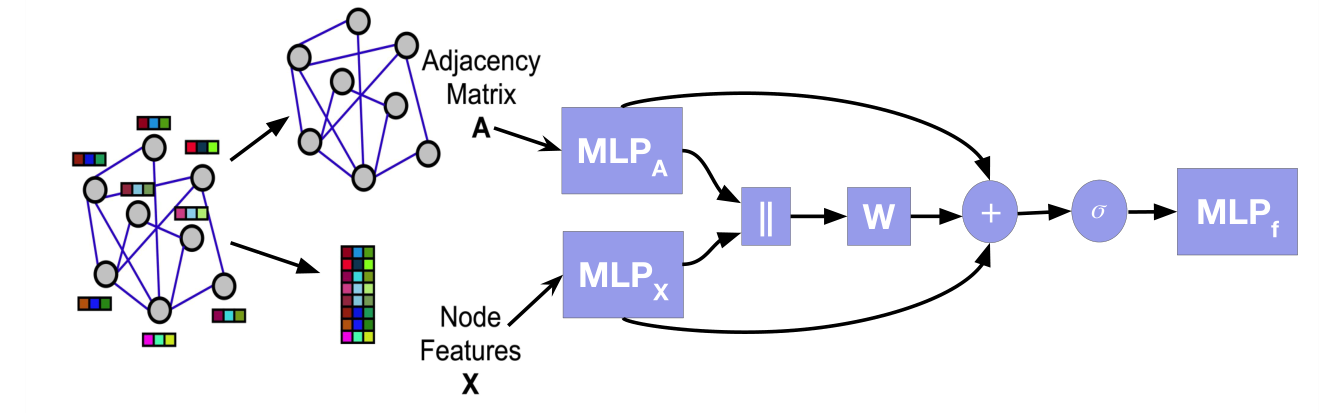
LINKX是一个看起来很简单的模型，是基于MLP，并没有作卷积操作。它首先将结点的特征矩阵与邻接矩阵经过分别经过2个MLP，然后再做一个连接，接着与参数矩阵\(W\)相乘，和前面经过MLP层的输出（类似于ResNet）

相加，接着经过一个激活函数和MLP，输出结果。

Gnnautoscale: Scalable and expressive graph neural networks via historical embeddings^[7]

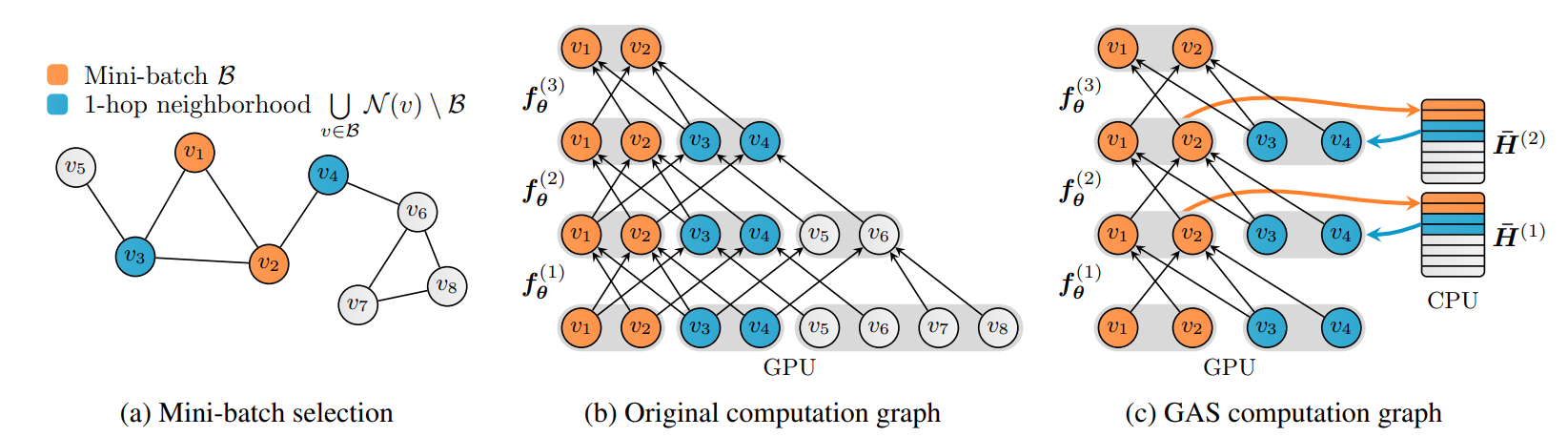
改论文主要聚焦于如何减小大型图数据训练的计算和内存开销。

GAS 框架有两个主要组成部分：

首先，第一部分是构建一个小批量节点（执行快速随机子采样）并修剪 GNN 计算图以仅保留小批量内的节点及其 1 跳邻居节点——这意味着 GAS 的尺度独立于 GNN 深度。其次，每当 GNN 聚合需要小批量节点嵌入时，GAS 就会从存储在 CPU 上的历史嵌入中检索它们。同时，当前小批量节点的历史嵌入也不断更新。

第二部分是与子采样的关键区别——能够使 GNN 最大限度地表达信息，并将当前的小批量数据和历史嵌入组合起来，得到完整的邻域信息并加以利用，同时确保对大型图的可扩展性。

GAS 的作者还将他们的想法整合到流行的 PyTorch 几何库中。于是可以在非常大的图上训练大多数的消息传递 GNN，同时降低 GPU 内存需求并保持接近全批次的性能（即在全图上训练时的性能）。

参考资料

1. Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016. ↩︎
2. Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017. ↩︎
3. Xu K, Hu W, Leskovec J, et al. How powerful are graph neural networks?[J]. arXiv preprint arXiv:1810.00826, 2018. ↩︎
4. Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs[J]. Advances in neural information processing systems, 2017, 30. ↩︎
5. Li X, Zhu R, Cheng Y, et al. Finding Global Homophily in Graph Neural Networks When Meeting Heterophily[J]. arXiv preprint arXiv:2205.07308, 2022. ↩︎
6. Lim D, Hohne F, Li X, et al. Large scale learning on non-homophilous graphs: New benchmarks and strong simple methods[J]. Advances in Neural Information Processing Systems, 2021, 34: 20887-20902. ↩︎
7. Fey M, Lenssen J E, Weichert F, et al. Gnnautoscale: Scalable and expressive graph neural networks via historical embeddings[C]//International Conference on Machine Learning. PMLR, 2021: 3294-3304. ↩︎