谱聚类

谱聚类

本文主要对谱聚类的几篇论文进行解读，并对一部分的结果进行复现。本文首先从谱聚类的一般过程入手，介绍传统的谱聚类方法NCuts、NJW。针对传统方法的相似度量的缺陷，引入改进方法ZP；又针对特征向量的选择问题，引入改进方法PI。结合以上2种方式，加入TKNN，引入改进方法ROSC，接着对ROSC中修正相似度矩阵的缺陷，结合trace lasso正则项，引入改进方法CAST。最后，对于ROSC和CAST中都提到的Group Effect进行解读。文章结尾补充了幂代法和矩阵求导的内容。其中我分别对PI方法和ROSC方法进行代码复现。

代码的仓库地址：https://github.com/vitaminzl/SpectralCluster

备用镜像：https://gitee.com/murphy_z/spectral-cluster

Pipeline

谱聚类的一般过程如上图所示[2]。对于一系列的数据，我们首先计算数据之间的相似度矩阵$S$，常用的相似度度量为高斯核$S_{ij}=\exp(-\frac{||\vec x_i-\vec x_j||^2}{2\sigma^2})$，然后求其拉普拉斯矩阵$L=D-S$，其中$D$为对角矩阵，且$D_{ii}=\sum A_{ij}$。然后求出拉普拉斯矩阵的特征向量，选择特征值$k$小的特征向量进行k-means聚类。

以上过程可以理解为，将原数据利用相似度度量转化为图数据，即使得每个数据间连着一条”虚边“，相似度即为边的权重。接下来将数据转换到频域上，选择一些低频作为数据的特征向量，这是因为低频成分往往具有更高层次、更具信息量的特征，而高频成分则更可能是噪声。然后对这些特征向量进行聚类。

而这种一般的方法在多尺度的数据聚类中往往表现不佳。

NCuts

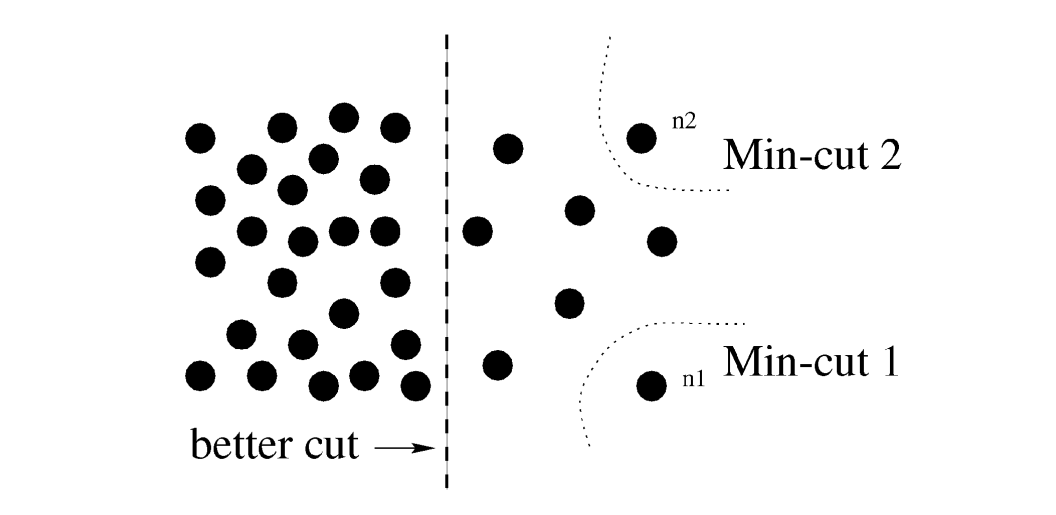
我们首先介绍一些远古的谱聚类方法。Normalized Cut[8]的想法来源于最小割。如果存在连通图$\mathcal G={\mathcal V, \mathcal E}$，每条边$e_i\in \mathcal E$有着权重$w_i$，为了使得连通图分割成2个连通子图，那么需要移掉一些边。若移掉这些边权之和最小，那么我们称这样的分割方法为最小割。这和聚类非常相似，边权可以表示点和点的联系，若存在两个类，那么类之间的联系应当是比较小的，类内的联系比较大。

所以一种可行的想法是，首先对连通图进行一次取最小割，然后再对连通子图进一步地取最小割，直到到达某一阈值为止。但显然这样存在一个问题，如上图所示，要使去掉边权之和最小，那每次分割肯可能都会倾向于指割掉一条边，这自然不合理。

一种自然的想法使对权重进行归一化处理
$$
NCut(A,B)=\frac{cut(A,B)}{assoc(A,V)}+\frac{cut(A,B)}{assoc(B,V)}
$$
其中$assoc(A,V)$表示$A$到所有连接的结点权重之和，$cut(A,B)$则是分割后移掉边权之和。所以假如当某一侧的结点非常少时，那么这$cut$的值可能比$assoc$大，极端情况下值分割一个点，那么分母就是0了，则最后的结果是无穷大。

因此利用前面的想法，每次使用$NCut$，然后再对子图进行$NCut$，不断进行二分就可以了。

听起来很简单，但很遗憾的是，求最小割是一个NP难的问题，因此只能求其近似解。

通过一系列的复杂推导（太难了哈哈），可以得到$D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$第2小的特征向量就是对应的最小割。当然这里需要设定一个阈值，因为特征向量求出来是浮点数，但其数据会偏向两级。然后利用上面的二分法求解即可。

但是现在多数使用的NCuts是$\min NCut(A,B)$问题转化为以下优化问题。
$$
\min \vec x^T(D^{-\frac{1}{2}}LD^{-\frac{1}{2}})\vec x\
st. \vec x^T\vec x=1
$$
上面这个形式其实就是瑞丽熵，那么只要取$k$个最小的特征值对应的特征向量进行聚类即可。

NJW

NJW算法[6]是取3个人名的首字母命名的。该算法和NCuts非常类似，甚至可以看作是其变形。
$$
\begin{align*}
D^{-\frac{1}{2}}LD^{-\frac{1}{2}}&=D^{-\frac{1}{2}}(D-S)D^{-\frac{1}{2}}\
&=I-D^{-\frac{1}{2}}SD^{\frac{1}{2}}
\end{align*}
$$
所以我们可以转而去求$D^{-\frac{1}{2}}SD^{\frac{1}{2}}$最大的$k$个特征向量，然后进行聚类。

ZP

前面提到计算相似度矩阵时，我们常用高斯核$S_{ij}=\exp(-\frac{||\vec x_i-\vec x_j||^2}{2\sigma^2})$，而高斯核中$\sigma$的选取是需要考虑的，很多时候常常人工设定[3]。但更重要的是$\sigma$是一个全局的参数，这在多尺度数据中具有一些缺陷。如设定的值较大时，稠密图的数据会趋于相似，设定较小时，稀疏图的数据则相似度过小。

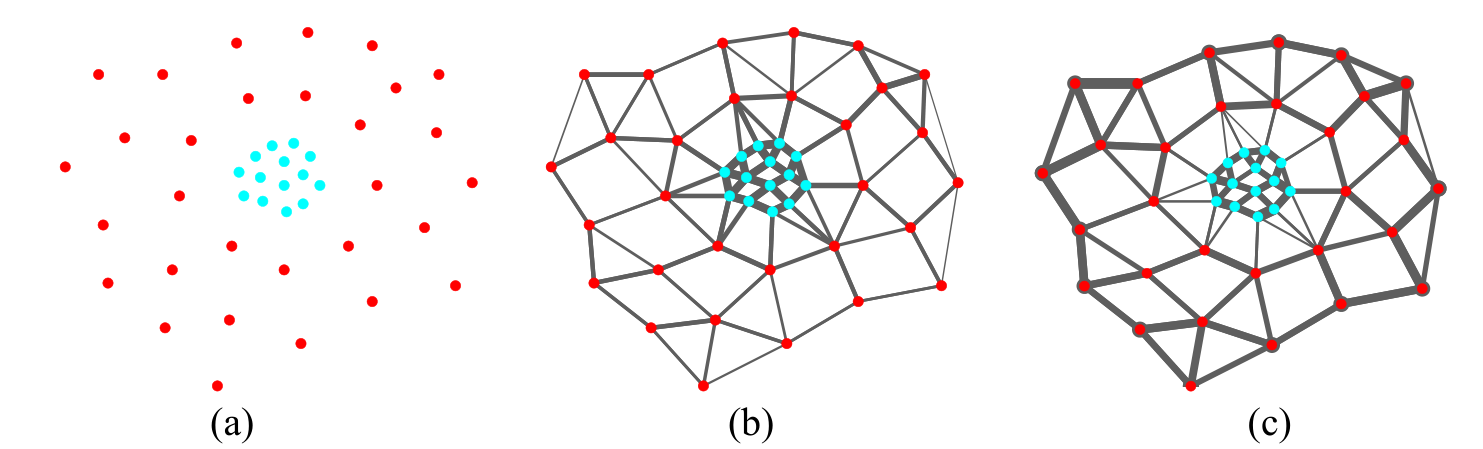
ZP方法提出里一种局部调整$\sigma$的设定，距离度量修正为$S_{ij}=\exp(-\frac{||\vec x_i-\vec x_j||^2}{2\sigma_i\sigma_j})$。其中$\sigma_i, \sigma_j$是依附于$\vec x_i, \vec x_j$的是一种局部的参数。这一参数的设定应通过样本的特征取选取。在论文中[3]中选择的方法是$\vec x_i$到第$K$个邻居的欧式距离，实验表明$K$取7在多个数据集上的效果表现良好。如上图所示，结点之间的边厚度表示数据间的权重大小（仅显示周围数据的权重）。图b是原来的高斯核距离度量，图c是修正后的。可以看到图b中靠近蓝点的边仍然比较厚，而图c则避免了的这种现象。

PI

PI(Power Iteration)为幂迭代法[5]。其灵感来源于幂迭代法用求主特征值（在[文章的后面部分](##Dominant Eigenvalue)会更详细地说明）。

我们设$W=D^{-1}A$，该矩阵有时候叫转移矩阵，因为它和马尔可夫的状态转移矩阵非常类似。每行的和为1，每个元素$W_{i,j}$可以看作是$i$结点到$j$结点转移的概率。它和归一化随机游走矩阵$L_r=I-W$有着重要的联系。NCuts算法证明了$L_r$第2小的特征值所对应的特征向量可以作为NCuts算法的一种近似。

这里需要说明的是，$L_r$最小的特征值为0，容易证明$\vec 1=[1, 1, …, 1]$是$L_r$的0所对应的特征向量。而对于$W$来说则，其最大的特征值为1，且$\vec 1$是对应的特征向量。需要说明的是，$L_r$最小的几个特征向量或$W$最大的几个特征向量是有效的，其余可能是噪声。

首先给定一个向量$\vec v^{(0)}= c_1\vec e_1 + c_2\vec e_2,…, +c_n\vec e_n$，其中$\vec e_i$为$W$的特征向量。且$\vec e_i$所对应的特征值$\lambda_i$满足$1=\lambda_1 > \lambda_2>…>\lambda_n$。

$$
\vec v^{(t+1)} = \frac{W\vec v^{(t)}}{||W\vec v^{(t)}||_1}
$$
假如我们按照如上的迭代公式进行迭代，则有如下过程（暂且忽略迭代公式的分母归一化项）
$$
\begin{align*}
\vec v^{(1)} &= W \vec v^{(0)}
\&=c_1W\vec e_1 + c_2W\vec e_2,…, +c_nW\vec e_n
\&=c_1\lambda_1 e_1 + c_2\lambda_2\vec e_2,…, +c_n\lambda_n\vec e_n
\end{align*}
$$
则
$$
\begin{align*}
\vec v^{(t)} &= Wv^{(t−1)} = W^2v^{(t−2)} = … = W^tv^{(0)}
\&=c_1W^t\vec e_1 + c_2W^t\vec e_2,…, +c_nW^t\vec e_n
\&=c_1\lambda_1^t e_1 + c_2\lambda_2^t\vec e_2,…, +c_n\lambda_n^t\vec e_n
\&=c_1\lambda_1^t\bigg[e_1+\sum\frac{c_2}{c_1}\bigg(\frac{\lambda_i}{\lambda_1}\bigg)^t\vec e_i)\bigg]
\end{align*}
$$
当$t\rightarrow +\infty$时，$\frac{c_2}{c_1}(\frac{\lambda_i}{\lambda_1})^t$会趋向于0。该方法的提出者认为，在有效成分$\vec e_i$的$\lambda_i$往往会接近于$\lambda_1$，而高频的一些噪声成分$\lambda_j$会接近于0。在迭代过程中使得有效成分$\vec e_i$前面的权重和噪声成分前的权重的差距会迅速扩大。

但是迭代的次数不宜过多，因为最后的结果会趋向于$k\vec 1$，因为$W$的主特征向量就是$\vec 1$。因此我们需设置一个迭代的门限值，以截断迭代过程。具体的算法如下。

这里以论文中开始提到的3圆圈数据集为例子，进行结果的复现，如下图所示。

通过以上的算法，我选取几次的迭代结果$\vec v^{(t)}$进行可视化，同一个类别在后面的迭代过程中逐渐局部收敛到一个值。

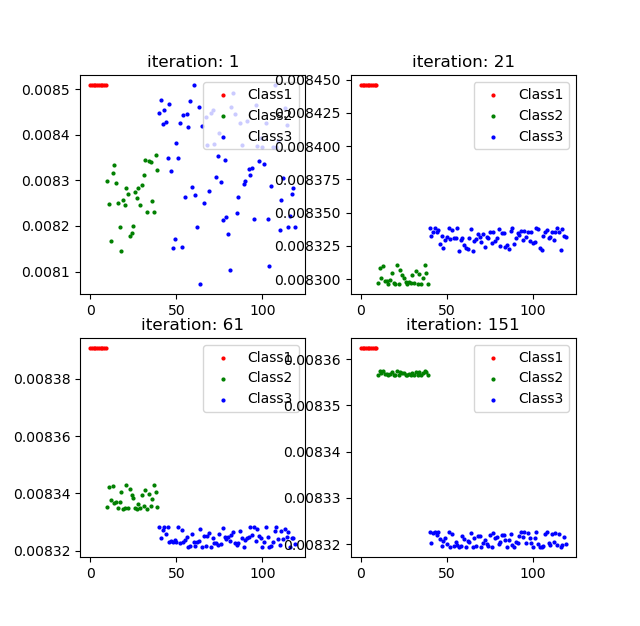
在实验中发现，其结果和许多因素有关，其中包括高斯核距离度量中的$\sigma$，初始的向量$\vec v^{(0)}$（论文中取$\vec v^{(0)}= \frac{\sum_j A_{ij}}{\sum_i\sum_j A_{ij}}$），结束时的$\hat\epsilon$设置，甚至发现使用$W^T$具有更好的效果，这是因为$W^T$的主特征值的特征向量就已经具有分类的效果（其意义尚待研究），而$W$的主特征向量是$\vec 1$，但这仅仅针对于3圆圈这一数据集而言。在问题与总结中，会提到这一点。此外还有计算机的运算精度也会影响结果。

该方法的一个重要优点是简单高效，其收敛速度快，在百万级别的数据中也能在几秒内收敛。缺陷是过分拔高了特征值大的部分，在多尺度数据中存在一些低特征值但仍然重要的信息。

以下是主函数的代码，完整代码见：https://github.com/vitaminzl/SpectralCluster/blob/master/PI.py

1
2
3
4
5
6
7
def main():
    data, labels = get3CircleData(radius=[0.1, 6, 17], nums=[10, 30, 80])
    draw3CircleData(x=data[:, 0], y=data[:, 1], labels=labels, title="Data Set")
    S_mtx = getSimilarMatrix(data, sigma=1.8)
    W = np.diag(1 / np.sum(S_mtx, axis=0)) @ S_mtx
    v_t = PowerIter(W, iter_nums=300, eps=1e-5, labels=labels)
    plt.show()

TKNN

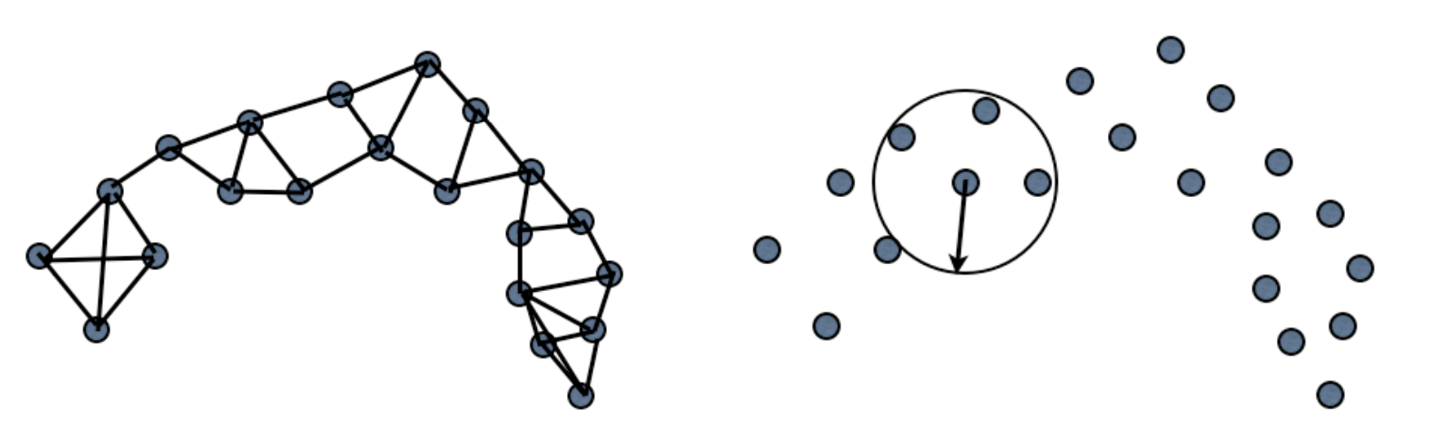
聚类问题转化为图问题时，需要解决邻接问题。定义结点之间的连接常常有2种方式[4]。第一种如上图左，每个数据选择自己最近的K个邻居相邻接，得到的图被称为K邻接图（K Nearest Neighbor Graph）；第二种如上图右，每个结点选择半径$\epsilon$的邻居相邻接。

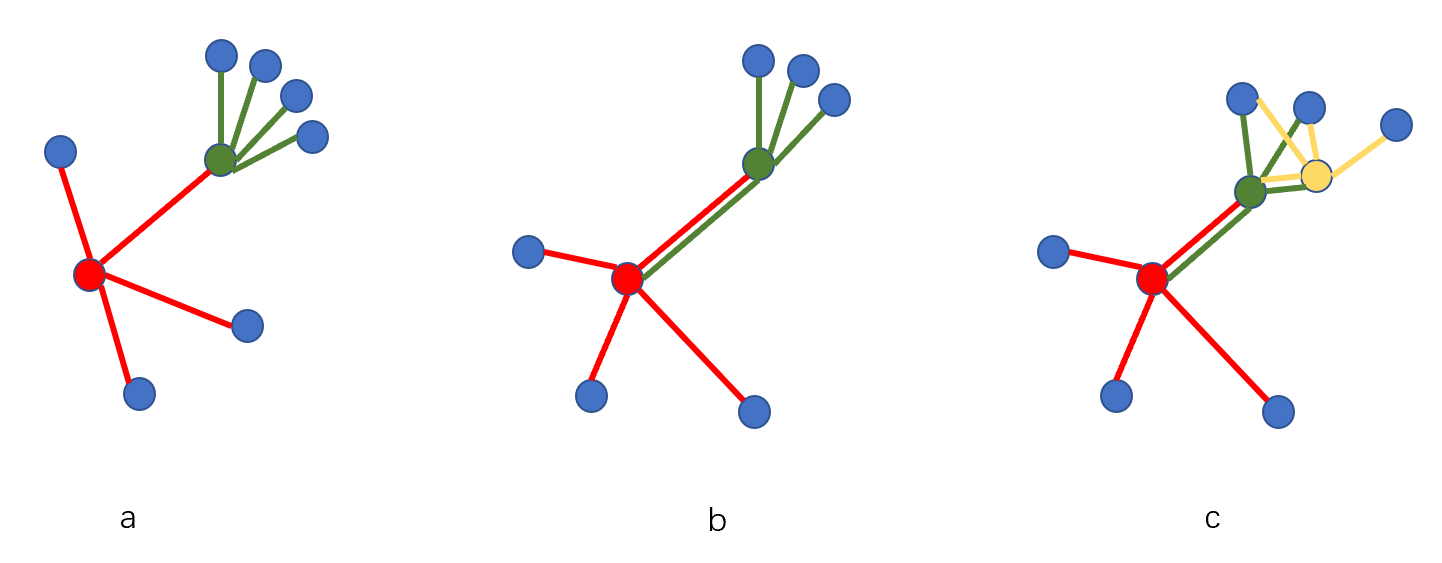
假如我们使用KNN的方法，K取4。如上图a所示，红色结点的4个最近邻用红线连接，绿色结点的4个最近邻用绿线连接。我们会发现，虽然红色的最近邻包括绿色，但绿色不包括红色，我们称红色和绿色不是相互近邻。但如图b所示，则红色和绿色则为相互近邻。若2个结点是相互近邻，则称这2个结点相互可达。如图c所示，红色与绿色是相互近邻，绿色和黄色相互近邻，那么红色和绿色也相互可达。

Transitive K Nearest Neighbor(TKNN) Graph 是指当2个结点时相互可达的，则二者连接一条边。因此其邻接矩阵$W$中，若2个点$i,j$相互可达，$W_{i,j}=W_{j,i}=1$。

构造的过程可描述如下：

  • step1: 构造K邻接矩阵$A$，对于结点$i$由$k$个邻居$j$，则$A_{i, j}=1$
  • step2: 构造相互近邻矩阵$A’=A A^T$，若为相互近邻，则为1，否则为0。
  • step3: 寻找$A’$的所有连通分量$S$
  • step4: 对于连通分量$S_i$中的每2个元素$S_{i,j}, S_{i,k}$，令$W_{S_{i,j},S_{i,k}}=W_{S_{i,k},S_{i,j}}=1$，其余为0。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def getTKNN_W(S_mtx, K):
    N = S_mtx.shape[0]
    KNN_A = np.zeros((N, N), dtype=np.int32)
    for i in range(N):
        idx = np.argsort(S_mtx[i, :])
        KNN_A[i, idx[(N-K):]] = 1
    MKNN_A = KNN_A * KNN_A.T
    G = nx.from_numpy_array(MKNN_A)
    compo_list = [c for c in nx.connected_components(G)]
    TKNN_W = np.zeros((N, N), dtype=np.int32)
    for c_i in compo_list:
        c = np.array(list(c_i), dtype=np.int32)
        idx_c = np.tile(c, (len(c), 1))
        TKNN_W[idx_c.T, idx_c] = 1 - np.identity(len(c))

    return TKNN_W

ROSC

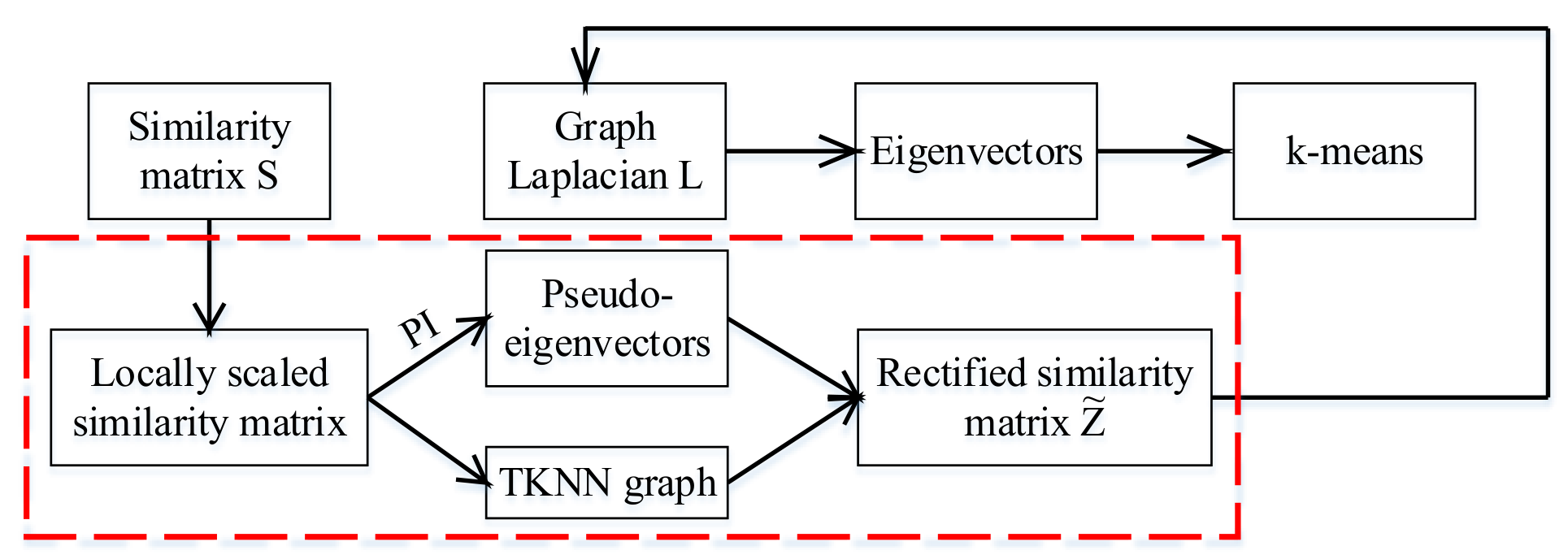
如上图所示为ROSC方法的流程图。ROSC方法[1]结合了以上2种方法，但相比于PI方法不同的是，它并不是将PI得到的输出直接作为k-means聚类的输入，而是增加了一个求修正相似矩阵的过程。

首先随机设置不同的$\vec v^{(0)}$获取$p$个“伪特征向量”，拼成一个$p\times n$的矩阵矩阵$X$，并对$X$进行标准化，即使得$XX^T=I$。

ROSC论文中认为，相似度矩阵的意义可以表示为某一个实体能够被其他实体所描述的程度。即任何一个实体$x_{i}=\sum Z_{i,j}x_j$，这里$Z_{i,j}$即为修正相似度矩阵。因此就有：
$$
X=XZ+O
$$
其中$O$表示噪声矩阵。

定义优化问题
$$
\min_{Z}||X-XZ||_F^2+\alpha_1||Z||_F+\alpha_2||W-Z||_F
$$
优化问题的第一项表示最小化噪声，第二项则是$Z$的Frobenius 范数[12]），为正则化项，用于平衡其他2项，第三项则是减小与前文中TKNN的邻接矩阵$W$的差距。$\alpha_1,\alpha_2$是平衡参数，需要人工设置。

求解以上优化问题，可以先对$Z$求导（[文章的后面](##Derivatives of Matrix)还会做一些补充），使导数为0即可。对三项项求导有
$$
\begin{align*}
\frac{\partial ||X-XZ||^2_F}{\partial Z}&=-2X^T(X-XZ)\
\frac{\partial\alpha_1||Z||^2_F}{\partial Z}&=2\alpha_1Z\
\frac{\partial\alpha_2||W-Z||^2_F}{\partial Z}&=-2\alpha_2(W-Z)
\end{align*}
$$
三项相加有
$$
-X^T(X-XZ)+\alpha_1Z-\alpha_2(W-Z)=0
$$
整理可得
$$
Z^*=(2X^TX+\alpha_1 I+\alpha_2 I)^{-1}(X^TX+\alpha_2W)
$$
但这样求出来的$Z^*$可能使不对称的，且可能存在负数。所以这里再次做了一个修正$\tilde Z=(|Z^*|+|Z^*|^T)/2$。

接下来就可以执行一般的谱聚类方法了。具体的算法流程可以用如下图所示：

算法第4行中的whiten为白化处理[9]，是数据预处理的一种常用方法。它类似于PCA，但与PCA不同的是，PCA往往用来降维，而白化则是利用PCA的特征向量，将数据转换到新的特征空间，然后对新的坐标进行方差归一化，目的是去除输入数据的冗余信息。

根据上述算法，以下使用python对其进行复现。

1
2
3
4
5
6
7
8
9
10
def ROSC(S, C_k, t_k, alpha1, alpha2):
    W_tknn = getTKNN_W(S, K=t_k)
    W = np.diag(np.sum(S, axis=0)) @ S
    X = prep.PIC_k(W, k=C_k)
    X = prep.whiten(X)
    X = prep.norm(X)
    Z = getROSC_Z(X.T, W_tknn, alpha1, alpha2)
    Z = (np.abs(Z) + np.abs(Z.T)) / 2
    C = postp.ncuts(Z, C_k)
    return C

主函数的代码如下

1
2
3
4
5
6
7
8
9
def main(data_name):
    path = "dataset/" + data_name + ".txt"
    data = np.loadtxt("dataset/Syn.txt", delimiter=',', dtype=np.float64)
    label = np.loadtxt("dataset/SynLabel.txt", dtype=np.int32)
    C_k = len(set(label))
    S = prep.getSimilarMatrix2(data=data)
    C = ROSC(S, C_k=C_k, t_k=t, alpha1=1, alpha2=0.01)
    prt, AMI, RI = postp.assess(label_true=label, label_pred=C)
    print(f"{data_name}\nPurity: {prt}\nAMI: {AMI}\nRI: {RI}\n")

完整代码见https://github.com/vitaminzl/SpectralCluster/blob/master/ROSC.py

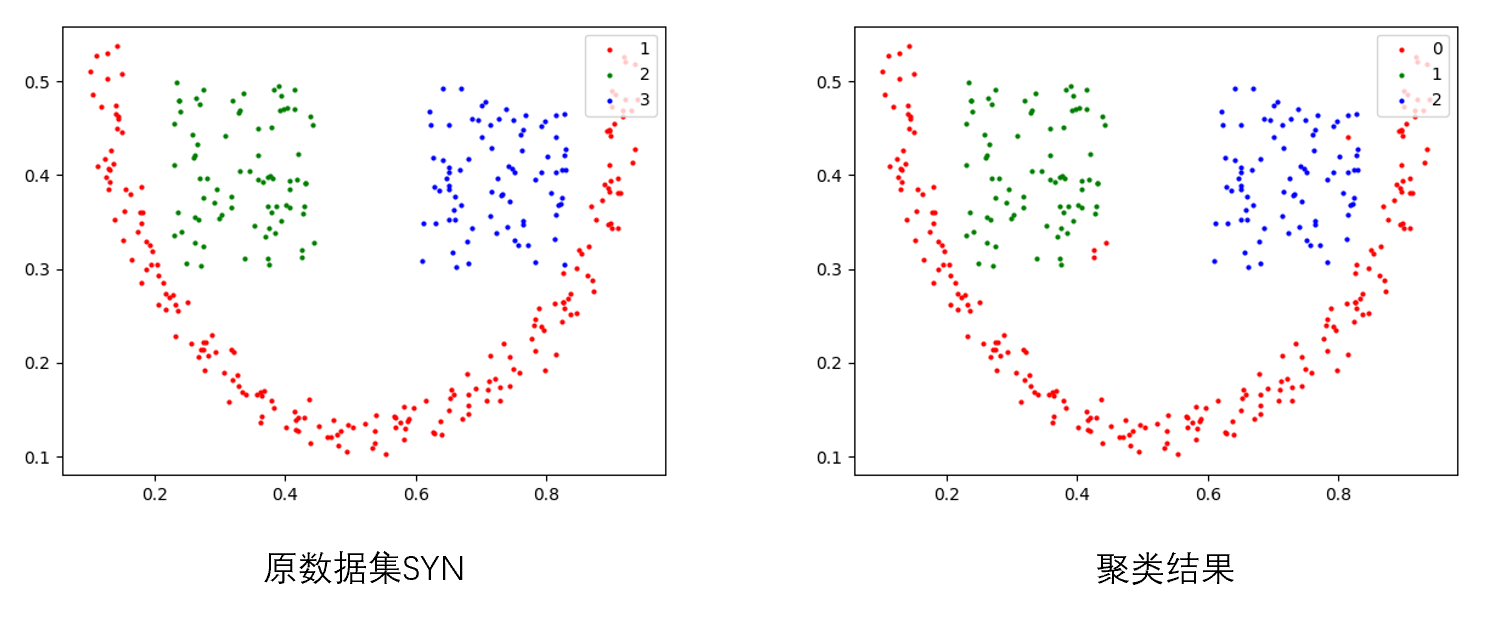
我首先使用了人工合成的数据集，如上图左所示。使用论文中的参数效果并不是很好，然后调整了一下求解TKNN矩阵的K，原文使用的是4，我调整为8，结果效果猛增，甚至优于论文的结果，如上图右所示，只有极个别点分错。不过根据数据集调参还是不科学的哈哈哈😂。其中Purity=0.9861，AMI=0.9307，RI=0.9784。

然后我对TKNN的K参数从1到12开始调整，3个指标的变化曲线如下图所示。感觉变化还是蛮明显的。

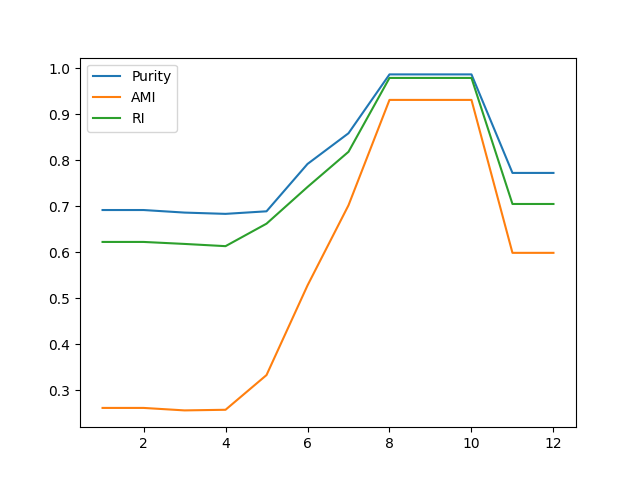
以下是5个数据集的实验结果，参数除了TKNN是的K是8以外，其他都和原论文相同，即$\alpha_1=1,\alpha_2=0.01$。大部分的数据集都没有论文的结果好（比论文结果好的加了粗），但也相差不多。除了MNist0127这个数据集是例外，其结果异常地差劲，也不知道是什么原因。

数据集 Purity AMI RI
COIL20 0.8486 0.9339 0.9683
Glass 0.6074 0.2949 0.7233
MNIST0127 0.2767 0.0156 0.3981
Isolet 0.7067 0.6151 0.8459
Yale 0.5636 0.3215 0.7704

Trace Lasso

Trace Lasso[13]是一种介于L1和L2正则的正则化项。其形式为
$$
\Omega(W)=||XDiag(W)||*
$$
其中$X$为已归一化的特征矩阵，即对于特征$\vec x_i$有$\vec x_i \vec x_i^T=1$。$W$为待求参数。$||·||$为核范数[14]（或迹范数）,$||Z||_=tr(\sqrt{Z^TZ})$，表示所有奇异值之和。

Trace Lasso具有如下性质：

  • 当$X^TX=I$时，即特征之间的相关性为0，或者正交，那么
    $$
    \Omega(W)=||W||_1
    $$
    即退化为1范式。

  • 当$X^TX=\vec 1^T\vec 1$时，即所有特征都完全相关，那么
    $$
    \Omega(W)=||W||_2
    $$
    即退化为2范式

  • 其他情况下，在1范式和2范式之间。

Trace Lasso的优点就是它可以根据数据的特征，接近合适的范式，这相比弹性网络更好。

CAST

ROSC方法虽然可以加强类内数据的联系，但没有使得类间的间距增大。

而CAST相比于ROSC的区别就在于修改了优化函数[2]，成为如下形式：
$$
\min_{Z} \frac{1}{2} ||\vec x-X\vec z||2+\alpha_1||XDiag(\vec z)||*+\frac{\alpha_2}{2}||W-\vec z||_2
$$
其中$\vec x$是$X$的其中一个特征向量，$z$是修正相似度矩阵$Z$中的一个向量。于ROSC的主要区别在于范数的选择，通过trace lasso可以使得其具有类内聚合也有类外稀疏的特性。

该优化问题的求解已经超出了我的能力范围，在此直接贴出论文中的算法流程

整个CAST算法的流程如下：

对比ROSC，他们的区别就在于求解$Z^*$的方法不同，其余都是一样的。

由于Inexcat ALM的算法超出了我的知识范畴，并且最近事情较多，CAST算法的代码并没有复现。若后面有时间再填补空缺。

Group Effect

Group Effect在ROSC和CAST论文中都提及了，以及一篇关于GNN的论文[7]中也提及了，可以说精髓所在了。

首先定义一些符号：若有一系列的实体$X={x_1,x_2,…,x_n}$，设$w_q$为$W$的第$q$列，设$x_i\rightarrow x_j$表示，$x_i^Tx_j\rightarrow 1$且$||w_i-w_j||_2\rightarrow 0$。

如果矩阵$Z$满足当$x_i\rightarrow x_j$时，有$|Z_{ip}-Z_{jp}|\rightarrow 0$，则称$Z$具有Group Effect。

翻译成人话就是当2个实体足够接近，$Z$矩阵中实体对应的元素也足够的接近。这说明了$Z$矩阵确实能够反映实体之间的联系紧密程度。2个实体足够接近，它可以指实体的特征足够接近，也可以指实体附近的结构接近。事实上在另一篇关于GNN的论文[7]里还包括了实体附近的结构信息。

可以证明的是，ROSC和CAST中的稀疏矩阵都有Group Effect，证明的过程过于复杂，也超出了我的能力范围了😂。

补充

Dominant Eigenvalue

若一个方阵$A$存在一系列特征值$\lambda_1,\lambda_2,…,\lambda_n$，且满足$|\lambda_1|>|\lambda_2|\ge…\ge|\lambda_n|$，则称$\lambda_1$为该方阵的主特征值[10]。前文中的幂迭代法原本就是用来求主特征值的。
$$
\begin{align*}
A^kq^{(0)} &= A^{k-1}q^{(1)} = … =Aq^{(k−1)}
\&=a_1A^k\vec e_1 + a_2A^k\vec e_2,…, +a_nA^k\vec e_n
\&=a_1\lambda_1^k e_1 + a_2\lambda_2^k\vec e_2,…, +a_n\lambda_n^k\vec e_n
\&=a_1\lambda_1^k\bigg[e_1+\sum_{i=2}^{n}\frac{a_i}{a_1}\bigg(\frac{\lambda_i}{\lambda_1}\bigg)^k\vec e_i)\bigg]
\end{align*}
$$
经过一系列迭代后又如上式子。显然，当$k\rightarrow\infty$时，$q^{(k)}=Aq^{(k−1)}=A^kq^{(0)}\rightarrow a_1\lambda^kx_1$。并且$[q^{k}]^TAq^{(k)}\approx [q^{(k)}]^T\lambda q^{(k)}=\lambda|q^{(k)}|_2=\lambda$，当$|q^{(k)}|_2=1$。所以每次迭代需要对$q$进行一次标准化。这样通过经过式子就可求出主特征值了。

Derivatives of Matrix

矩阵求导是矩阵论中的相关知识[11]，这里仅对前文用到的Frobenius范式矩阵的求导过程进行介绍。

Frobenius范式可以表示成如下的迹形式
$$
||X||_F=\sqrt{tr(X^TX)}
$$
首先引入2个求导法则

  • 法则1：若$A,X$为$m\times n$的矩阵，有
    $$
    \frac{\partial tr(A^TX)}{\partial X}=\frac{\partial tr(X^TA)}{\partial X}=A
    $$

  • 法则2：若$A$为$m\times m$的矩阵，$X$为$m\times n$的矩阵，有

$$
\frac{\partial tr(X^TAX)}{\partial X}=AX+A^TX
$$

因此若求以下导数
$$
\frac{\partial ||A-BX||^2_F}{\partial X}
$$
利用以上法则有：
$$
\begin{align*}
\frac{\partial||A-BX||^2_F}{\partial X}&=\frac{\partial tr[(A-BX)^T(A-BX)]}{\partial X}\
&=\frac{\partial tr[(A^T-X^TB^T)(A-BX)]}{\partial X}\
&=\frac{\partial[tr(A^TA)-2tr(A^TBX)+tr(X^TB^TBX)]}{\partial X}\
&=0-2A^TB+B^TBX+B^TBX\
&=-2B^T(A+BX)
\end{align*}
$$

问题与总结

在这次深入解读论文的过程中，有很多收获，学到了很多，但也发觉不明白的东西也很多。实验中也遇到各种问题，比如在PI方法的实验中，发现对$W^T=D^{-1}S$的最小特征向量在3圆圈数据集中，具有明显的分层，其分层特征和类别基本一致，这是一次代码写错时发现的。以及论文中出现了非常多优化问题求解，也触及到了很多知识盲区。但同时也激发了我的求知欲望，需要学的东西还有很多。

参考资料

  1. Li X, Kao B, Luo S, et al. Rosc: Robust spectral clustering on multi-scale data[C]//Proceedings of the 2018 World Wide Web Conference. 2018: 157-166. ↩
  2. Li X, Kao B, Shan C, et al. CAST: a correlation-based adaptive spectral clustering algorithm on multi-scale data[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020: 439-449. ↩
  3. Zelnik-Manor L, Perona P. Self-tuning spectral clustering[J]. Advances in neural information processing systems, 2004, 17. ↩
  4. https://csustan.csustan.edu/~tom/Clustering/GraphLaplacian-tutorial.pdf ↩
  5. Lin F, Cohen W W. Power iteration clustering[C]//ICML. 2010. ↩
  6. Ng A, Jordan M, Weiss Y. On spectral clustering: Analysis and an algorithm[J]. Advances in neural information processing systems, 2001, 14. ↩
  7. Li X, Zhu R, Cheng Y, et al. Finding Global Homophily in Graph Neural Networks When Meeting Heterophily[J]. arXiv preprint arXiv:2205.07308, 2022 ↩
  8. Shi J, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22(8): 888-905. ↩
  9. https://en.wikipedia.org/wiki/Whitening_transformation ↩
  10. https://www.cs.huji.ac.il/w~csip/tirgul2.pdf ↩
  11. Petersen K B, Pedersen M S. The matrix cookbook[J]. Technical University of Denmark, 2008, 7(15): 510. ↩
  12. https://mathworld.wolfram.com/FrobeniusNorm.html ↩
  13. Grave E, Obozinski G R, Bach F. Trace lasso: a trace norm regularization for correlated designs[J]. Advances in Neural Information Processing Systems, 2011, 24. ↩
  14. https://en.wikipedia.org/wiki/Matrix_norm ↩
谱图理论
#频域 #python #聚类 #谱聚类 #多尺度数据
谱聚类
http://vitaminzl.com/2022/08/30/gnn/spectral-cluster/
作者
vitaminzl
发布于
2022年8月30日
许可协议