图（Graph）数据的频域

图（Graph）数据的频域

图神经网络（GNN）是近年来愈发火热，用以对图（Graph）数据进行特征提取以及各种下游任务。注意这里的图（Graph）应和图像（Image）区分，图是一种由点集与边集组成的数据结构，常记作$\mathcal{G}=(\mathcal{V,E})$。以下是我学习谱图理论时的一些记录。本文先先从基变换的角度入手，说明了标准正交基的性质，并从实数域拓展到了复数域，接着从基变换的角度阐述了傅里叶变换的原理，然后从特征值与特征向量入手，通过分析拉普拉斯算子的特征向量，理解其与傅里叶变换的等价性。最后使用图的数据结构表示图像，可视化其特征向量，直观感受低频到高频分量的差异。本人才疏学浅，错误难免，欢迎交流指正。

内积与基

我们首先回顾一下线性代数的知识。本科第一次线性代数的时候，都是以繁杂的计算与证明为主，未曾有更直观、直觉的方式去理解。这里我想从线性变换的角度，讲述线性代数中与本文内容相关的知识。

我们定义实数向量$\vec x=[x_1, x_2,…,x_n]^T$与实数向量的$\vec x=[x_1, x_2,…,x_n]^T$内积为$<\vec x,\vec y>=\sum x_iy_i$。这是高中就学过的知识。但这里，我需要对向量的内积做一些扩充，即复数向量内积的定义。根据hermitian内积的定义[1]，复平面内积定义为$<\vec x,\vec y>=\sum x_i\bar y_i$。

如果我们将向量内积扩展到函数空间，我们可以将函数视为无限长的向量，如$f(x)=[f(x_1),f(x_2),…]$，可以定义函数的内积[2]$<f,g>=\int_a^b f(x)g(x)dx$。若函数在复平面上，则可定义为$<f,g>=\int_a^b f(x)\overline{g(x)}dx$（有时共轭会放在左边）。

然后我们来回顾一下向量空间中的基。由一组线性无关的向量可以张成一个向量空间，空间中的任意向量都可以使用这一组向量的线性组合表示。这组向量称作基向量。如果基向量构成的矩阵$A=[\vec\alpha_1,\vec\alpha_2,…,\vec\alpha_n]^T$满足$AA^T=E$，则这组基向量称为正交基，若还满足$||\vec\alpha_i||=1,(i=1,2,…,n)$，则称为标准正交基。如，二维向量$[1,0]^T,[0,1]^T$构成一组标准正交基。在复平面中[6]，转置被描述为$(A^H){ij}=\overline{A{ji}}$，相比实数域，处了转置还要做一次共轭，称为共轭转置。那么正交基构成的矩阵$A$应满足$AA^H=E$。

假如有标准正交基$\vec e_1, \vec e_2,…,\vec e_n$，若该空间中向量
$$
\vec v=w_1\vec e_1+w_2\vec e_2+,…+w_n\vec e_n=[\vec e_1,\vec e_2,…, \vec e_n][w_1,w_2,…,w_m]^T
$$
则
$$
[w_1,w_2,…,w_m]^T=[\vec e_1,\vec e_2,… ,\vec e_n]^{-1}\vec v=[\vec e_1,\vec e_2,… ,\vec e_n]^{T}\vec v
$$
可以看到，若想获得一组某向量在一组标准正交基上的表示，只需要让该向量与这组正交基做内积即可。

函数也存在着基的概念，若函数$f(x)=a_ng(x)+b_nh(x)$。那么$g(x)$和$h(x)$就是$f(x)$的基。若内积$<g,h>=0$，$g$和$h$是一组正交基。

傅里叶变换

在学习傅里叶变换时，想必类似上面的图大家已经见过很多次了，这里我们暂且不从几何的角度去解释，从基的角度去阐述。大多数教材都会先从傅里叶级数入手，周期函数可以表示为许多正弦信号的叠加，有如下形式
$$
f(t)=\frac{a_0}{2}+\sum_{n=1}^{+\infty} [a_n\sin(\frac{n\pi}{l} t )+b_n\cos({\frac{n\pi}{l} t})]
$$
其中，$n$是整数，$l$为半周期。$1,\sin(n\omega t ),\cos({n\omega t})$可以看作是$f(t)$许许多多相互正交的基。这是因为[3]：$\int^{\pi}{-\pi}\cos nxdx=0$,$\int^{\pi}{-\pi}\sin nxdx=0$, $\int^{\pi}{-\pi}\cos n_1x\sin n_2xdx=0$, $\int^{\pi}{-\pi}\cos n_1x\cos n_2xdx=0$,$\int^{\pi}_{-\pi}\sin n_1x\sin n_2xdx=0$。

如果使用Euler公式替换， 可以转换为如下形式
$$
f(t)=\sum^{+\infty}{n=-\infty}c_ne^{i\omega t}
$$
其中，$c_n=\frac{1}{l}\int{-l}^{l}f(t)e^{-i\omega t}dt$。$l$为半周期，$\omega=\frac{n\pi}{l}$，即频率（有些地方会将$\omega$视作角速度，指数项写作$e^{2i\pi\omega t}$）。这里$e^{i\omega t}$也是许多的标准正交基，这是因为$\int e^{i\omega_1 t}e^{-i\omega_2 t}=0$，$||e^{i\omega}||=1$。那么当$l\rightarrow +\infty$时，$c_n$就是傅里叶变换的形式了。即
$$
\mathcal{F}[f(t)]=\hat f(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}dt
$$
所以像函数$\hat f(\omega)$其实就是$\omega$对应的傅里叶基$e^{i\omega t}$的系数。上述式子也可以看作是$f(t)$与正交基$e^{i\omega t}$的内积，在上一节中提到了，若某个向量希望使用某组正交基来表示，拿就让这个向量和这组标准正交基做内积，标准正交基就像一个筛子，把基方向的分量提取出来了。

在计算机中，使用离散傅里叶变换（DFT）的算法计算：被描述为[8]
$$
X_k=\sum_{n=0}^{N-1}x_n \cdot e^{-\frac{i2\pi}{N}kn}
$$
实际计算时如快速傅里叶变换（FFT），使用如下DFT矩阵[9]与向量$\vec x=[x_1,x_2,…,x_n]^T$相乘。
$$
W = \frac{1}{\sqrt{N}} \begin{bmatrix}
1&1&1&1&\cdots &1 \
1&\omega&\omega^2&\omega^3&\cdots&\omega^{N-1} \
1&\omega^2&\omega^4&\omega^6&\cdots&\omega^{2(N-1)}\ 1&\omega^3&\omega^6&\omega^9&\cdots&\omega^{3(N-1)}\
\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\
1&\omega^{N-1}&\omega^{2(N-1)}&\omega^{3(N-1)}&\cdots&\omega^{(N-1)(N-1)}
\end{bmatrix}
$$
其中$\omega = e^{-2\pi i/N}$。易证明$WW^H=E$，即它由一组标准正交基构成。具体的计算方法使用快速傅里叶变换，可以将复杂度降至$O(n\log n)$，具体过程可以参考[4]。

特征值与特征向量

简单地回顾一些特征值与特征向量的定义，设有矩阵$A$，若存在$\lambda,\vec x$，使得$A\vec x=\lambda \vec x$，则$\lambda$称为$A$的特征值，$\vec x$则称为特征向量，$\lambda$的值可以不止一个，同一个$\lambda$可以对应多个线性无关的$\vec x$。如果想了解特征值与特征向量的几何解释，可以参考[5]，这不是本文的重点。

接下啦我想说明的是一种特殊的矩阵：实对称矩阵，即由实数组成的对称矩阵（若$A=A^T$则称$A$为对称矩阵）。该矩阵有很多优良的性质。首先，$N$阶是对称矩阵，具有$N$个特征值以及$N$个正交的特征向量。且实对称矩阵一定可以相似对角化，即$Q^{-1}AQ=Q^TAQ=\Lambda$。对角矩阵$\Lambda$对角线上为特征值$\lambda_1,\lambda_2,…$，分别对应$Q=[\vec q_1, \vec q_2,…]$中的特征向量$\vec q_1,\vec q_2,…$。

由于其$Q$由一组线性无关的正交特征向量组成，他们可以构成一组正交基，特征向量组成的基也成为特征基。我们举个相似对角化的简单应用。假如要求实对称矩阵$A$的幂次预算，如$A^{100}$。直接计算是很麻烦的，若首先将其转化为对角矩阵$Q^{-1}AQ=\Lambda$，那么$Q^{-1}AQ…Q^{-1}AQQ^{-1}AQ=Q^{-1}A^{100}Q=\Lambda^{100}$。则$A^{100}=Q\Lambda^{100}Q^{-1}$。对角矩阵的100次幂是非常容易计算的，这就使得计算量大大减小。

特征值与特征向量在微分方程中也有着重要应用[6]。如对一个一阶微分方程$\frac{du}{dt}=\lambda u$。它的特解为$e^{\lambda t}$，通解为$u(t)=Ce^t$。假如$A$是一个常数矩阵，$\vec u=[u_1,u_2,…,u_n]$。$\frac{d\vec u}{dt}=A \vec u$，那么这就是在求解一个微分线性方程组。我们可以验证的是（将以下2式子带入原方程就可以证得），当$A\vec x= \lambda \vec x$时，$\vec u$的一个特解为$\vec u = e^{\lambda t}\vec x$，$\vec x$是一个常数向量。那么解原方程组转化为求$A\vec x= \lambda \vec x$的问题求出特征值与特征向量，最后的通解即为$C_1e^{\lambda_1 t}\vec x_1+C_2e^{\lambda_2 t}\vec x_2,….$。

若我们将一阶微分记作$\nabla$，则$\frac{d\vec u}{dt} = \nabla \vec u$，带入一个特解可以得到$\nabla \vec u=\nabla e^{\lambda t}\vec x = \lambda e^{\lambda t}\vec x$。我们可以将$\lambda$视为$\Delta$的特征值，$e^{\lambda t}$为特征向量。假如是二阶微分方程$\frac{d^2\vec u}{dt^2}=A \vec u$，会有所不同，若满足$A\vec x= \lambda \vec x$，其特解为$\lambda e^{i\omega t} \vec x$，其中$\omega^2=-\lambda$。同上，若我们将二阶微分算子记为$\Delta$，则有$\Delta \vec u =\Delta e^{i\omega t}\vec x= \lambda e^{i\omega t}\vec x$。那么$e^{i\omega t}\vec x$就是$\Delta$的特征向量。

拉普拉斯矩阵

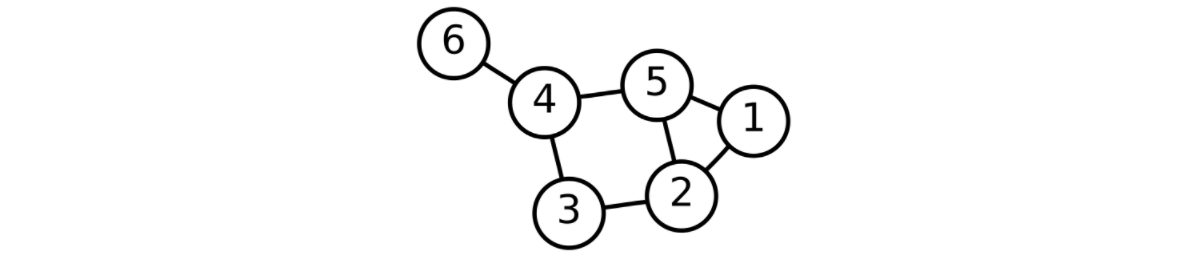
对于如上的图数据，它的拉普拉斯矩阵如下。其计算方法是$D-A$。$D$是每个结点的度组成的对角矩阵，$A$是图的邻接矩阵。
$$
L=\left(\begin{array}{rrrrrr}
2 & -1 & 0 & 0 & -1 & 0\
-1 & 3 & -1 & 0 & -1 & 0\
0 & -1 & 2 & -1 & 0 & 0\
0 & 0 & -1 & 3 & -1 & -1\
-1 & -1 & 0 & -1 & 3 & 0\
0 & 0 & 0 & -1 & 0 & 1\
\end{array}\right)
$$
拉普拉斯矩阵是拉普拉斯算子在图数据中的表示方式[10]，也被称为离散拉普拉斯算子。拉普拉斯算子是一个二阶微分算子，记作$\Delta f = \sum_{i=1}^n \frac {\partial^2 f}{\partial x^2_i}$，在上一节的结尾，我们其实提到了这个算子。它的特征向量其实就是傅里叶变换中的正交基。实际上，实际上函数的傅里叶变换是定义在所有欧几里得空间上的函数的分解到其在拉普拉斯算子连续谱中的分量[7]。

拉普拉斯矩阵是一个实对称矩阵，上一节中提到实对称矩阵的一些优良性质，存在标准正交基构成的矩阵$U$及其对应的特征值对角矩阵$\Lambda$使得拉普拉斯矩阵$L$满足$U^TLU=\Lambda$。其中$U=[\vec u_1, \vec u_2,…, \vec u_n]$中的$\vec u_i$可以视为离散的傅里叶基，而所对应的特征值则为频率。如果每个结点的特征（简单起见，每个结点只有一维特征）组成的向量$\vec x=[x_1,x_2,…,x_n]$，那么如果我们将其转化为频域向量$\vec y=U^T\vec x$，正如我们在第一节、第二节提到的方式一样。然后就可以在频域中操作，再转换为时域即可。

图的频域分量

在讲图（Graph）之前，我们可以先聊聊图像（Image）。图像通常由一个矩阵表示，矩阵中的每一个值为像素点的值。根据通道数，图像又可以分为彩色图像和灰度图像。

事实上图像它也可表示称图的结构。如下图所示[11]：

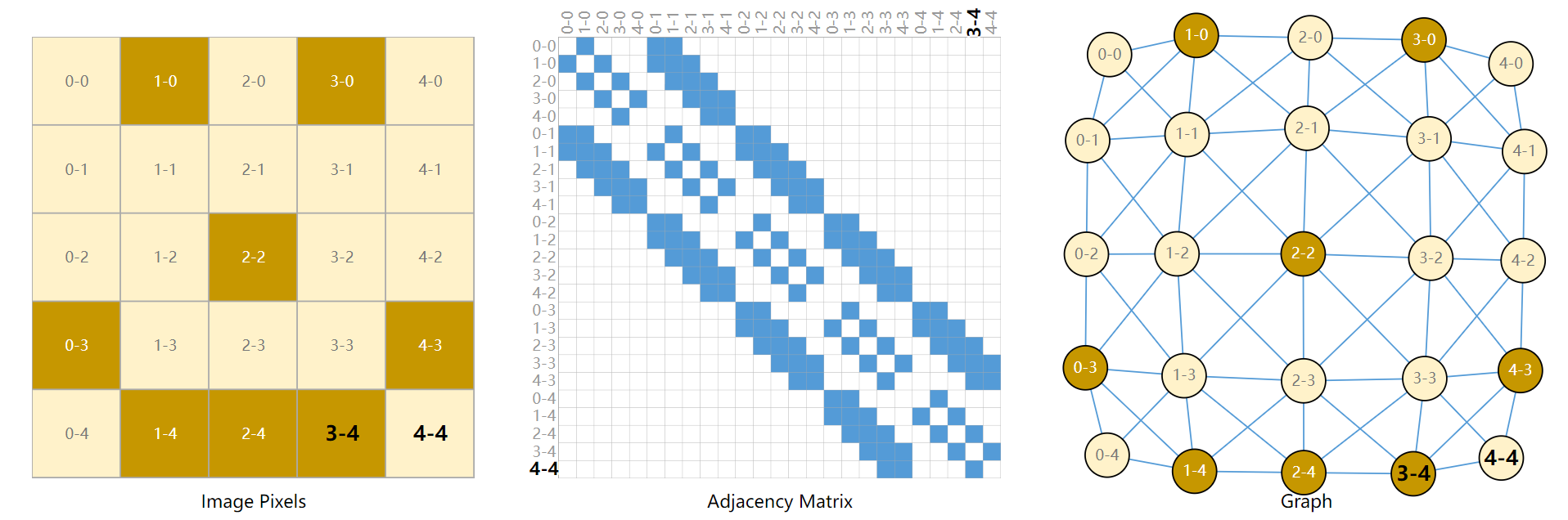
其中，每个像素与上下左右对角线相邻接。

为了方便可视化图数据的频域分量，我们使用上述图数据的结构，即讲图像转化为图。具体执行如下操作[12]：

  • step1. 选择(10, 10)尺寸的图像结构，
  • step2. 根据每个像素与上下左右对角线相邻接的规则构造邻接矩阵A, shape: (100, 10)
  • step3. 根据邻接矩阵A构造拉普拉斯矩阵L, shape: (100, 100)
  • step4. 对拉普拉斯矩阵进行对角化, 求得特征基矩阵U, shape(100, 100)，对角矩阵P, shape(100, 100)，注意上述2个矩阵均按特征值的大小升序排序。
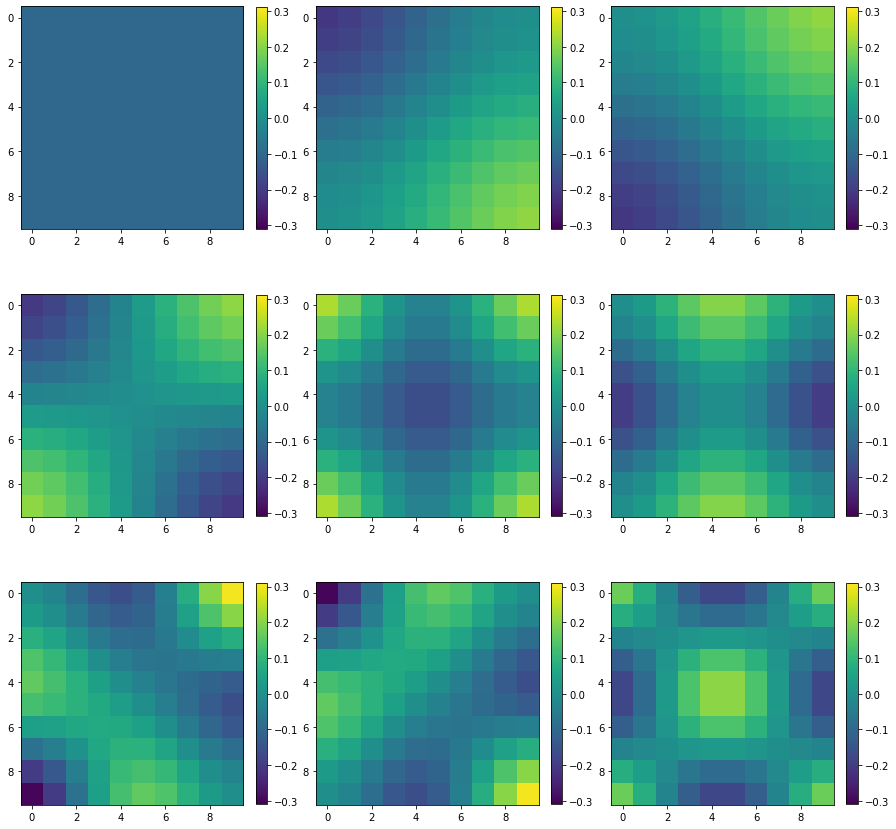
  • step5. 取特征值大小前10的特征基，每个特征基重构为图像结构Image, shape(10, 10)，进行可视化

经过以上的操作后，最后的结果如下图所示，特征值按从小到大排序。这就是每个频率所对应的分量。可以看到图像一开始是纯色的，后来开始出现了类似波形的渐变过程，随着频率的增加，其波形也越复杂。

以下为实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import math
import matplotlib.pyplot as plt

def getLaplacianOfImage(M, N):
    idx = np.array([i for i in range(M * N)]).reshape((M, N))
    tmp = np.ones((M+2, N+2), dtype=np.int32) * M * N
    tmp[1:M+1, 1:N+1] = idx
    # print(tmp)
    directH = [1, -1, 0, 0, 1, -1, 1, -1]
    directV = [0, 0, 1, -1, 1, -1, -1, 1]
    A = np.zeros((M * N + 1, M * N + 1))
    for i in range(1, M+1):
        for j in range(1, N+1):
            for h, v in zip(directH, directV):
                A[tmp[i, j], tmp[i+h, j+v]] = 1
    A = A[0:M*N, 0:M*N]
    L = np.diag(np.sum(A, axis=1)) - A
    return L

M, N = 10, 10
L = getLaplacianOfImage(M, N)
# print(L)
# print(np.prod(L == L.T))
# plt.imshow(L)
eigenvalue, featurevector = np.linalg.eigh(L)
eigenbase = featurevector.T

min_val, max_val = np.min(eigenbase), np.max(eigenbase)
plt.figure(figsize=(15, 15))
for i in range(9):
    fv = eigenbase[i].reshape((M, N))
    plt.subplot(3, 3, i+1)
    plt.imshow(fv, vmin=min_val, vmax=max_val)
    plt.colorbar(fraction=0.045)

总结

写该博客的起因是学习GNN时，不理解为什么使用$L$矩阵，而不是用邻接矩阵或者其他实对称矩阵，以及在文献中[13]看到$L$矩阵的谱分解其实就是傅里叶变换在图领域的应用。为了深入了解这二者的关系，捡起了以前学过但又未深入理解的知识。完成这篇博客，还是很有收获的。

参考资料

  1. https://mathworld.wolfram.com/HermitianInnerProduct.html ↩
  2. https://mathworld.wolfram.com/HilbertSpace.html ↩
  3. 同济大学数学系．高等数学 [M]，第七版，高等教育出版社，2014-07-04 ↩
  4. https://www.bilibili.com/video/BV1za411F76U?spm_id_from=333.337.search-card.all.click&vd_source=3eafcac5a31e0009a6433cea9bc7ab45 ↩
  5. https://www.bilibili.com/video/BV1ys411472E?p=14&vd_source=3eafcac5a31e0009a6433cea9bc7ab45 ↩
  6. https://math.mit.edu/~gs/linearalgebra/ ↩
  7. https://en.wikipedia.org/wiki/Hilbert_space#Fourier_analysis ↩
  8. https://en.wikipedia.org/wiki/Discrete_Fourier_transform ↩
  9. https://en.wikipedia.org/wiki/DFT_matrix ↩
  10. https://csustan.csustan.edu/~tom/Clustering/GraphLaplacian-tutorial.pdf ↩
  11. https://distill.pub/2021/gnn-intro/ ↩
  12. https://distill.pub/2021/understanding-gnns/#learning ↩
  13. Li X, Zhu R, Cheng Y, et al. Finding Global Homophily in Graph Neural Networks When Meeting Heterophily[J]. arXiv preprint arXiv:2205.07308, 2022. ↩
谱图理论
#频域 #谱图理论 #傅里叶变换 #线性代数 #python
图（Graph）数据的频域
http://vitaminzl.com/2022/08/20/gnn/tu-graph-shu-ju-de-pin-yu/
作者
vitaminzl
发布于
2022年8月20日
许可协议